归一化
 # 为什么要归一化
# 为什么要归一化
在机器学习领域,数据分布是很重要的概念。如果训练集和测试集的分布很不相同,那么在训练集上训练好的模型,在测试集上应该不奏效(比如用ImageNet训练的分类网络去在灰度医学图像上finetune再测试,效果应该不好)。对于神经网络来说,如果每一层的数据分布都不一样,后一层的网络则需要去学习适应前一层的数据分布,这相当于去做了domain的adaptation,无疑增加了训练难度,尤其是网络越来越深的情况。因此,只是对输入的数据进行归一化处理也是不够的,这样只能保证输入的数据分布一致,不能保证每层网络的输入数据分布一致,因此在神经网络的中间层也需要加入归一化操作。 # 归一化流程
- 计算出均值
- 计算出方差
- 归一化处理到均值为0,方差为1
- 变化重构,恢复出这一层网络所要学到的分布
\[ \begin{aligned} \mu_{\mathcal{B}} & \leftarrow \frac{1}{m} \sum_{i=1}^{m} x_{i} \\ \sigma_{\mathcal{B}}^{2} & \leftarrow \frac{1}{m} \sum_{i=1}^{m}\left(x_{i}-\mu_{\mathcal{B}}\right)^{2} \\ \widehat{x}_{i} & \leftarrow \frac{x_{i}-\mu_{\mathcal{B}}}{\sqrt{\sigma_{\mathcal{B}}^{2}+\epsilon}} \\ y_{i} & \leftarrow \gamma \widehat{x}_{i}+\beta \equiv \operatorname{BN}_{\gamma, \beta}\left(x_{i}\right) \end{aligned} \] 上式是BN的公式,前两行计算输入数据一个batch的均值与方差,之后均值、方差变换为0、1即标准正态分布,最后每个元素乘以 \(\gamma\) 再加上 \(\beta\) 得到输出, \(\gamma\) 和 \(\beta\) 是可训练的参数。 # 区别
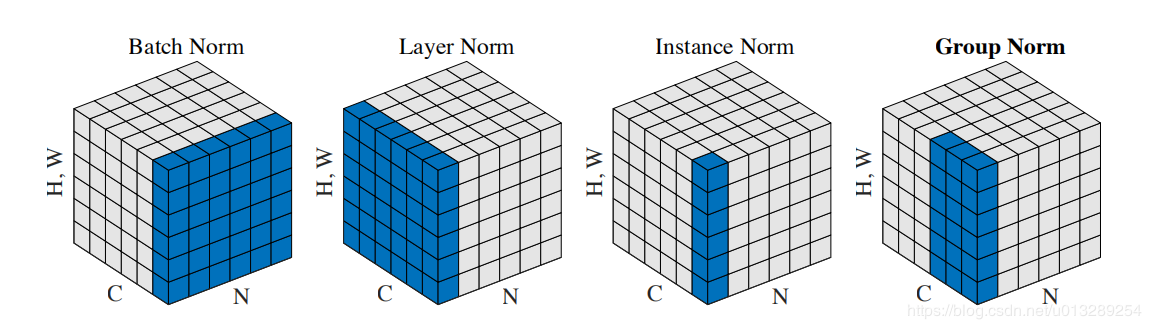
BN
BN的计算就是把每个通道的NHW单独拿出来归一化处理
针对每个channel我们都有一组γ,β,所以可学习的参数为2*C
当batch size越小,BN的表现效果也越不好,因为计算过程中所得到的均值和方差不能代表全局 ## LN
LN的计算就是把每个CHW单独拿出来归一化处理,不受batchsize 的影响
常用在RNN和Transformer,但如果输入的特征区别很大,那么就不建议使用它做归一化处理。主要是用于NLP,但CV中ViT和ConvNext也用了。 ## IN
IN的计算就是把每个HW单独拿出来归一化处理,不受通道和batchsize 的影响
常用在风格化迁移,但如果特征图可以用到通道之间的相关性,那么就不建议使用它做归一化处理 ## GN
GN的计算就是把先把通道C分成G组,然后把每个gHW单独拿出来归一化处理,最后把G组归一化之后的数据合并成CHW
GN介于LN和IN之间,当然可以说LN和IN就是GN的特列,比如G的大小为1或者为C