FR-Head

Posted on Edited on In

paper code

摘要

人类动作识别旨在从视频片段中分类人类动作的类别。最近，人们开始设计基于GCN的模型来从骨架中提取特征，以执行此任务，因为骨架表示比其他模态（如RGB帧）更有效且更稳健。然而，在使用骨架数据时，一些重要的线索如相关项也被丢弃了。这导致一些模糊的动作很难被区分并且容易被错误分类。为了缓解这个问题，我们提出了一个辅助特征细化头（FR Head），它包括空间-时间解耦和对比特征细化，以获取骨架的有区别的表示。模糊样本在特征空间中动态发现并校准。此外，FR Head可以强加在GCN的不同阶段，以构建更强的监督的多级细化。我们在NTU RGB+D、NTU RGB+D 120和NW-UCLA数据集上进行了大量实验。我们提出的模型获得了与最先进方法相竞争的结果，并且可以帮助区分这些模糊的样本。

引言

现有方法的问题

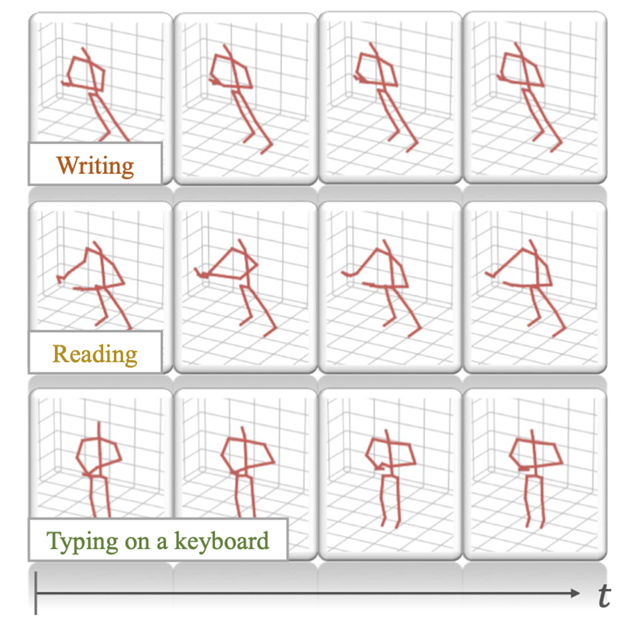
目前骨架表示缺乏对相似动作的重要交互对象和上下文信息，如下图，基于骨架视图很难区分“书写”、“阅读”和“键盘打字”。

相似动作 ## 解决方案

提出一个基于对比学习的特征细化模块，以提高在模糊动作之间的特征区分能力。首先将隐藏特征分解为空间和时间组件，使网络能够更好地专注于模糊动作之间的有区别的部分；然后，根据模型在训练过程中的预测，识别出确信和模糊的样本。确信的样本用于维护每个类别的原型，这通过对比学习损失来实现，以约束类内和类间距离。同时，模糊的样本通过在特征空间中更接近或远离确信的样本来进行校准。此外，上述特征细化模块可以嵌入到多种类型的GCNs中，以改进层次特征学习。它将产生一个多级对比损失，与分类损失一起进行联合训练，以提高模糊动作的性能。

贡献

  • 提出了一个有区别的特征细化模块，以提高基于骨架的动作识别中模糊动作的性能。它使用对比学习来约束确信样本和模糊样本之间的距离。它还以轻量级的方式将原始特征图分解为空间和时间组件，以实现有效的特征增强。
  • 该特征细化模块是即插即用的，并与大多数基于GCN的模型兼容。它可以与其他损失一起联合训练，但在推断阶段被丢弃。
  • 在NTU RGB+D、NTU RGB+D 120和NW-UCLA数据集上进行了大量实验，将提出的方法与最先进的模型进行比较。实验结果表明了提出的方法的显著改进。

方法

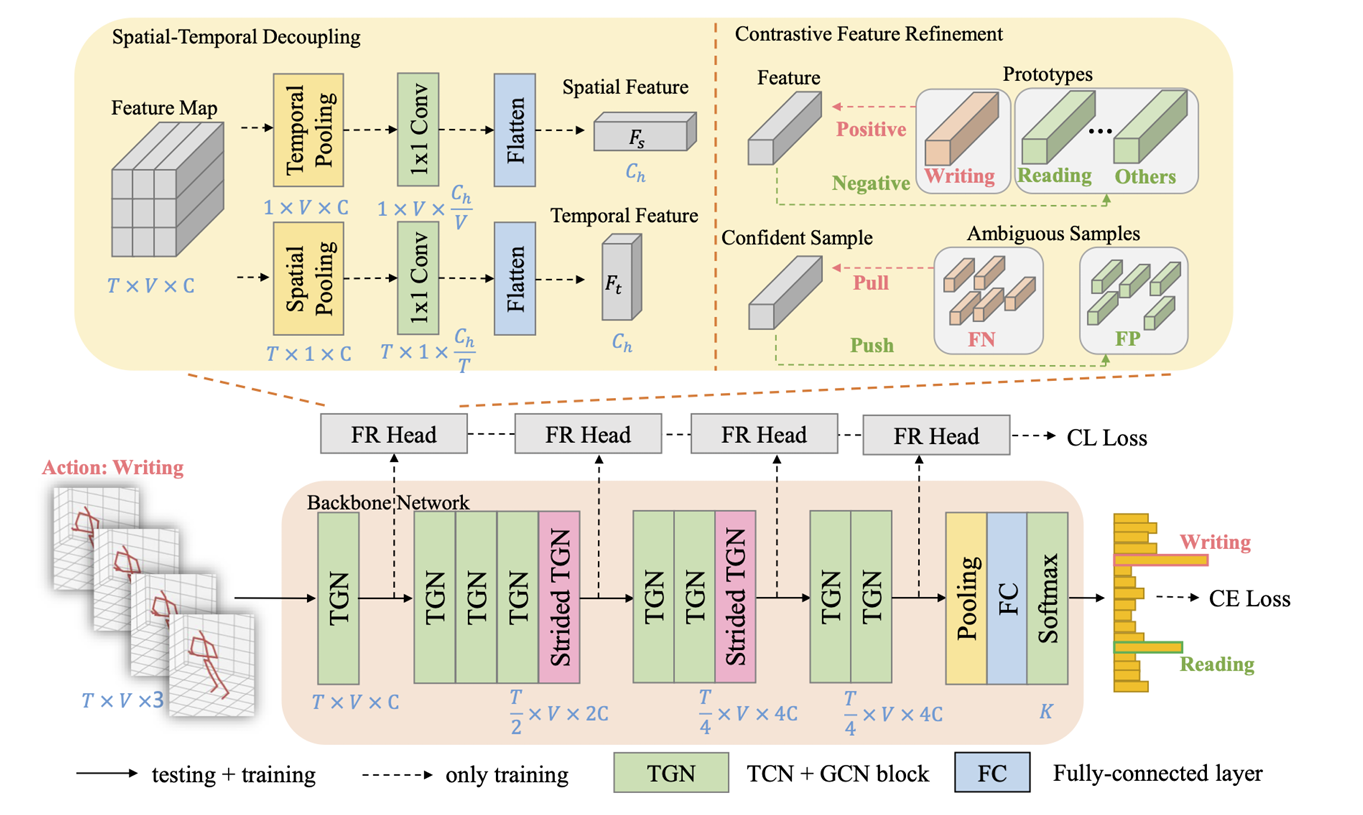Model overview 文章主要提出一种即插即用模块来优化骨干网中的多层次特征，称为特征细化头(FR Head)。

Multi-Level Feature Selection

论文将backbone分为四个阶段，分别位于TGN的第1、第5、第8和最后一层，并在每个阶段上加一个FR Head，而在第5和第8层采用了Strided操作。每个FR Head 会分别计算对比学习损失，并且每个阶段各有一个权重参数，从而得到一个总的CL Loss： \[ \begin{equation} \mathcal{L}_{CL} = \sum_{i=1}^{4} \lambda_i \cdot \mathcal{L}_{CL}^i \end{equation} \]

Spatial-Temporal Decoupling

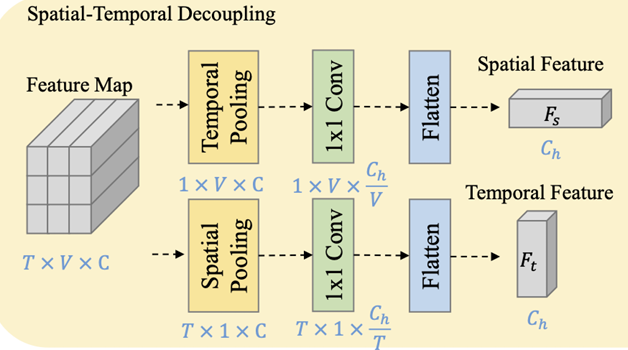
FR Head的第一部分为时空解耦模块，如下图，特征图通过两个不同的分支提取解耦的时空特征，具体通过不同维度的池化解耦时空特征，以及通过1x1卷积获得固定大小的特征，然后Flatten为通道大小为\(C_h\)的表示。最后计算出时间特征和空间特征的CL损失，相加以得到总损失：

\[ \mathcal{L}_{CL}^i = \text{CL}(F_s^i) + \text{CL}(F_t^i) \]

时空解耦

Contrastive Feature Refinement

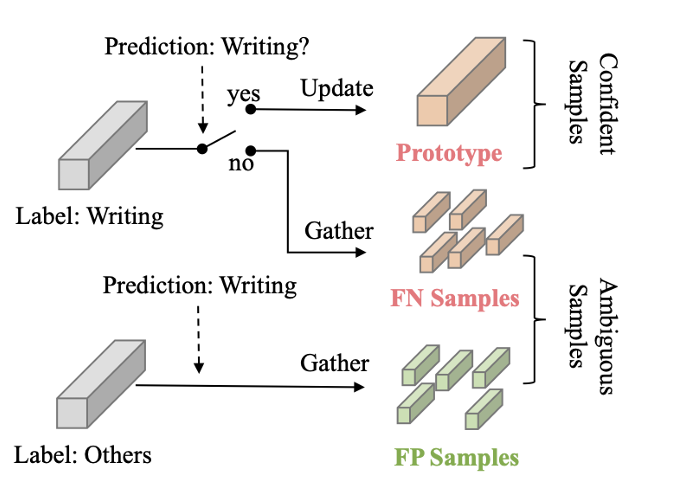
作者受RCH启发，采用对比学习的方法镜像特征细化，通过样本的基础真值动作和其他模糊动作改进样本的预测结果。 动作“书写”中自信样本和模糊样本的发现

Confident Sample Clustering

给定一个动作标签 \(k\)，如果一个样本被正确预测，即作为一个真正的正样本（TP），将其视为一个确信的样本，以区分它与模糊的样本，而显然确信样本的特征往往具有更好的类内一致性。通过指数移动平均来更新对应类的Prototype，即聚合对于动作标签\(k\)的可信样本特征以得到对应的global representation。假设 \(s_{TP}^k\) 是一个批次中动作 \(k\) 的确信样本的集合，其大小为 \(n_{TP}^k\)，EMA 操作可以定义为： \[ P_k = (1 - \alpha) \cdot \frac{1}{n_{TP}^k} \sum_{i \in s_{TP}^k} F_i + \alpha \cdot P_k \] 其中，\(P_k\) 是动作 \(k\) 的Prototype，\(F_i\) 是从样本 \(i\) 提取的特征。\(\alpha\) 是动量项，通过经验将其设置为 \(0.9\)。随着训练样本的增加，\(P_k\)会成为动作\(k\)的聚类中心，能对新到达的样本的特征进行区分，即每个样本应该接近相关的Prototype，同时远离其他Prototype，通过余弦距离来定义两个特征样本的距离： \[ \operatorname{dis}(u, v)=\frac{u v^{T}}{\|u\|_{2}\|v\|_{2}} \] ### Ambiguous Sample Discovering

给定一个动作标签 \(k\)，有两种类型的模糊样本。如果一个动作 \(k\) 的样本被错误地分类为其他类别，则称为假阴性（FN）。如果其他类别的样本被错误地分类为动作 \(k\)，则称为假阳性（FP）。假设 \(s_{FN}^k, s_{FP}^k\) 是动作 \(k\) 的FN和FP样本的集合，它们的大小分别为 \(n_{FN}^k, n_{FP}^k\)。在一个批次中收集这些样本，并计算均值作为中心表示：

\[ {\mu}^k_{FN} = \frac{1}{n^k_{FN}} \sum_{j \in s_{FN}^k} F_j,~~{\mu}^k_{FP} = \frac{1}{n^k_{FP}} \sum_{j \in s_{FP}^k} F_j \] 其中，\({\mu}^k_{FN}, {\mu}^k_{FP}\) 表示类别 \(k\) 的FN和FP样本的中心表示。但与确信样本不同，这些样本的预测在训练阶段不稳定，并且数量远少于TP样本，因此没有维护Prototype。

Ambiguous Sample Calibration

为了校准模糊样本的预测，将动作 \(k\) 的确信样本 \(i\) 作为锚点，并在特征空间中计算一个辅助项。对于那些应该被分类为动作 \(k\) 的FN样本，引入一个补偿项 \(\phi_i\)： \[   \phi_i = \left\{   \begin{aligned}     1 - \text{dis}(F_i, {\mu}^k_{FN}) &, \mbox{if } i \in s^k_{TP} \mbox{ and } n^k_{FN} > 0;\\      0 &, \mbox{otherwise}.\\   \end{aligned}   \right. \] 通过最小化补偿项 \(\phi_i\)，FN样本应该在特征空间中更接近确信样本。当没有FN样本或余弦距离收敛到1时，\(\phi_i\) 达到最小值 \(0\)。这可能会激励模型将这些模糊样本更正为动作 \(k\)。 另一方面，对于那些属于其他类别的FP样本，引入一个惩罚项 \(\psi_i\)： \[ \psi_i = \left\{ \begin{aligned} 1 + \text{dis}(F_i, {\mu}^k_{FP}) &, \mbox{if } i \in s^k_{TP} \mbox{ and } n^k_{FP} > 0;\\ 0 &, \mbox{otherwise}.\\ \end{aligned} \right. \] 类似地，惩罚项 \(\psi_i\) 对FP样本与确信样本在特征空间中的距离进行惩罚。当没有FP样本或余弦距离收敛到-1时，\(\psi_i\) 达到最小值 \(0\)。这可能会阻止模型将这些模糊样本识别为动作 \(k\)。 最后，以样本 \(i\) 为锚点，所提出的对比学习（CL）损失函数可以定义为： \[ \begin{split}   \text{CL}(F_i) = - \text{log} \frac{ e^{ \text{dis}(F_i, P_k) / \tau - (1 - p_{ik}) \psi_i }  }{ e^{ \text{dis}(F_i, P_k) / \tau - (1 - p_{ik}) \psi_i } + \sum_{l \neq k} e^{ \text{dis}(F_i, P_l) / \tau}  }  \\   - \text{log} \frac{ e^{ \text{dis}(F_i, P_k) / \tau - (1 - p_{ik}) \phi_i }  }{ e^{ \text{dis}(F_i, P_k) / \tau - (1 - p_{ik}) \psi_i } + \sum_{l \neq k} e^{ \text{dis}(F_i, P_l) / \tau}  }   \end{split} \] 其中，\(p_{ik}\) 是样本 \(i\) 对于类别 \(k\) 的预测概率得分。这意味着对于置信度较弱的TP样本，它们从这些模糊样本中获得了更强的监督。

Training Objective

Loss采用CELoss，再加上多级的CL loss，如下： \[ \mathcal{L}_{CE} = - \frac{1}{N} \sum_i \sum_c y_{ic} \mbox{log}(p_{ic}) \]

\[ \mathcal{L} = \mathcal{L}_{CE} + w_{cl} \cdot \mathcal{L}_{CL} \]

实验

消融实验

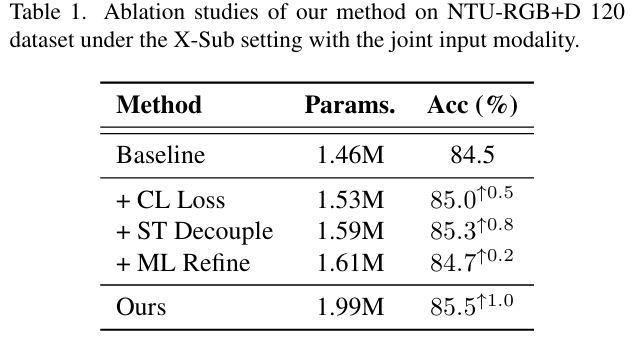image.png - CL Loss：直接使用CL损失来细化最后一层的特征，没有任何额外的操作 - ST Decouple：在细化之前将特征分解成空间和时间分量 - ML Refine：在训练管道中的多级阶段上施加细化

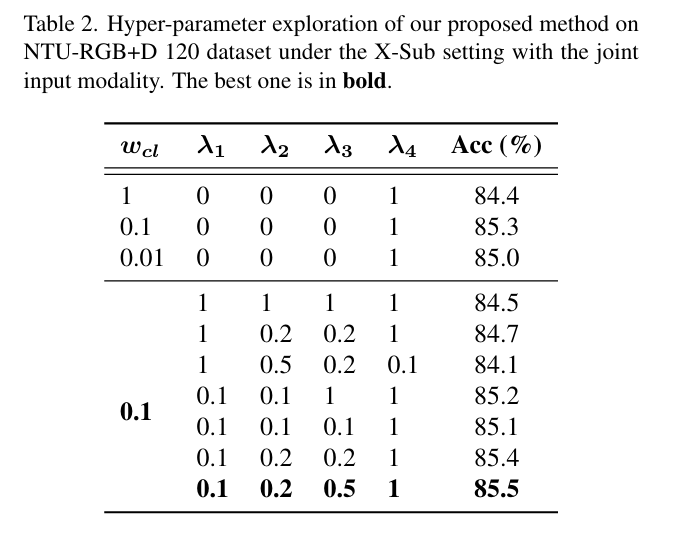image.png 作者尝试了 不同的 \(w_{cl}\) 值，以找到CL损失和CE损失之间的平衡；尝试了更多的 \(\lambda_i\) 组合来平衡不同阶段的重要性。从结果中，可以观察到给予先前层更高的权重可能会获得负面影响，而逐渐从早期阶段增加重要性到最后阶段，从而导致最佳结果。可以得出结论，来自最终阶段的高级特征的细化起主要作用，而低级特征提供辅助效果。

对比实验

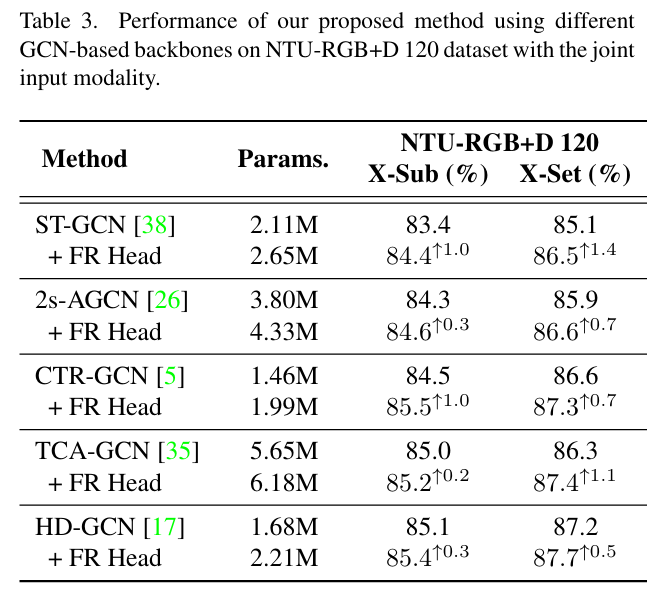
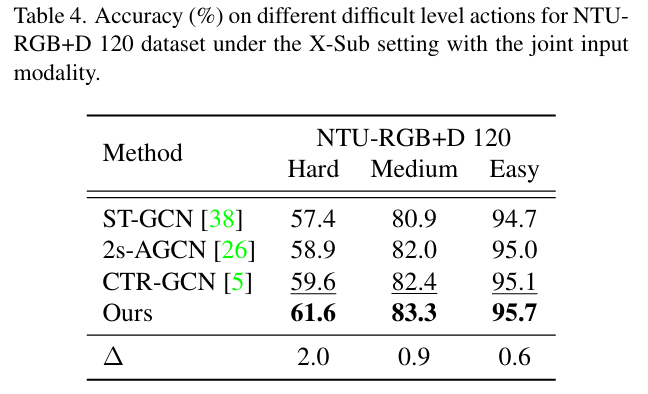
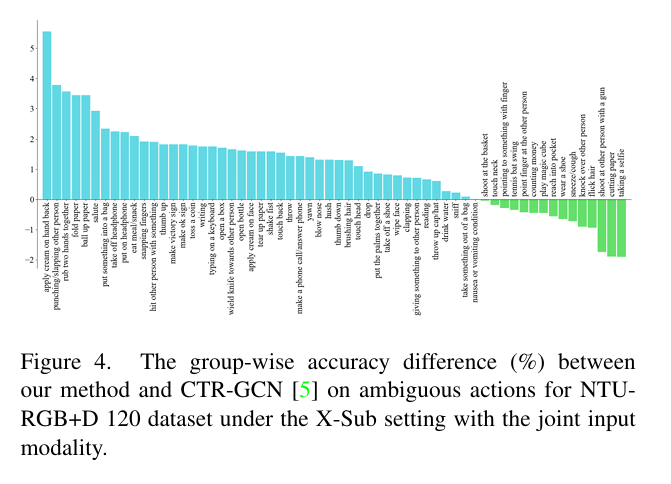
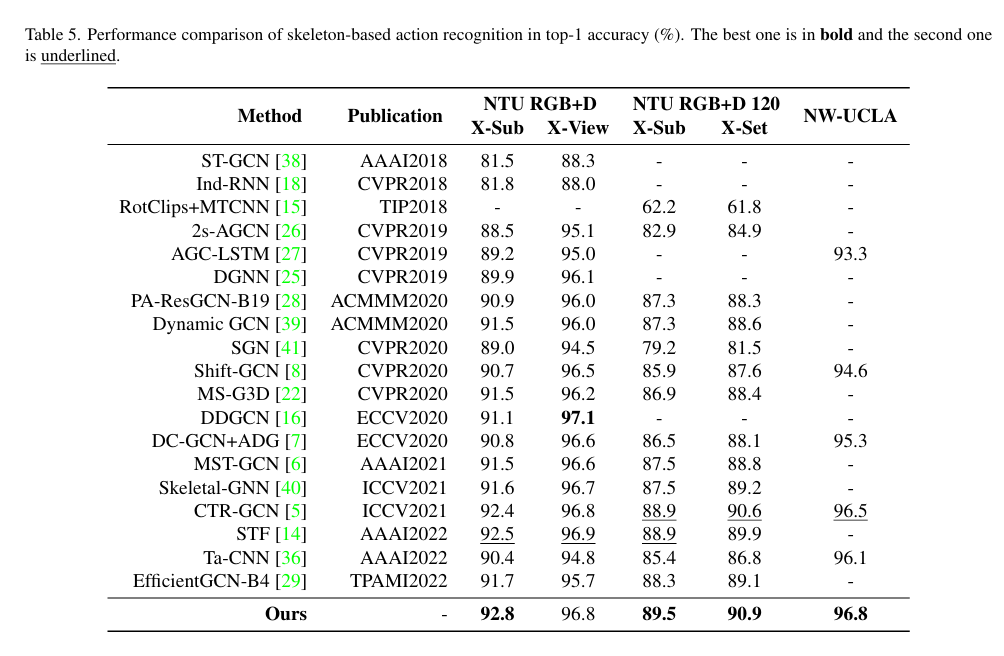
image.png image.png image.png image.png ## 与SOTA对比

image.png