Skeleton MixFormer

Posted on 2023-11-04 Edited on 2024-03-06 In 骨架动作识别

Skeleton MixFormer: Multivariate Topology Representation for Skeleton-based Action Recognition # 摘要

Vision Transformer在各种视觉任务中表现出色，但在基于骨架的动作识别中遇到了瓶颈，并且不及先进的基于图卷积网络（GCN）的方法。其根本原因在于当前的骨架变换器依赖于完整通道的全局关节的自注意机制，忽略了通道内高度区分性的差异相关性，因此难以动态学习多变拓扑的表达。为解决这一问题，我们提出了Skeleton MixFormer，这是一种创新的时空架构，能够有效表示紧凑的骨架数据的物理相关性和时间交互性。该提议框架由两个基本组成部分组成：1）空间MixFormer。利用通道分组和混合注意力计算动态的多变拓扑关系。与全通道自注意方法相比，空间MixFormer更好地突出了通道组之间的区别以及关节邻接的可解释学习。2）时间MixFormer，包括多尺度卷积、时间变换器和顺序保持模块。多变时间模型确保了全局差异表达的丰富性，并实现了序列中关键间隔的区分，从而更有效地学习动作中的长期和短期依赖关系。我们的Skeleton MixFormer在四个标准数据集（NTU-60、NTU-120、NW-UCLA和UAV-Human）的七种不同设置上展现出最先进（SOTA）的性能。

引言

论文背景: 人体动作识别是计算机多媒体处理领域中的一个基础且重要的课题，对于自动驾驶、视频监控、人机交互和端到端系统等领域提供可靠的以人为中心的动作分析结果。近年来，基于骨架的动作识别受到了广泛关注和发展。紧凑的骨架数据提供了人体关节的详细位置和运动信息，有助于构建时空运动并更加关注动作的基本特征。

过去方案: 传统的Transformer在图像和自然语言处理等视觉任务中表现出色，但在基于骨架的动作识别中遇到了瓶颈，并且无法超越先进的基于GCN的方法。这是因为当前的骨架Transformer依赖于全局关节的自注意机制，忽视了通道内高度区分性的差分相关性，因此难以动态学习多元拓扑的表达。此外，标准的Transformer架构缺乏关键帧提取模块，难以捕捉短期时间相关性的特征，可能导致性能下降。

论文的Motivation: 鉴于现有方法的局限性，本文提出了Skeleton MixFormer，通过引入Spatial MixFormer和Temporal MixFormer两个关键组件，有效地利用全局信息学习能力，克服了当前识别方法的限制，实现了更灵活的多元时空表示和更好的动作识别性能。

论文贡献：

• 提出了一种新颖的Skeleton MixFormer用于动作识别。该模型更灵活，通过依赖通道的内在关联来构建多变量时空表示，以最大限度地利用高度可区分的特征，并优化变换器对全局信息的依赖。

• 空间MixFormer挖掘了通道组之间的差异性关联，通过混合注意力实现了多变拓扑表达的动态学习，并丰富了骨架邻接关系的可解释性。

• 时间MixFormer整合了多尺度卷积、时间变换器和顺序保持模块，确保了全局时间特征的差异性和长期短期依赖的学习，为动作序列提供了有序且有效的更新。

• 在四个标准数据集（NTU-60、NTU-120、NW-UCLA、UAV-Human）上，Skeleton MixFormer在基于GCN和基于Transformer的方法中均取得了最高性能。充分的消融实验证明了所提出的架构的可解释性和可重复性。

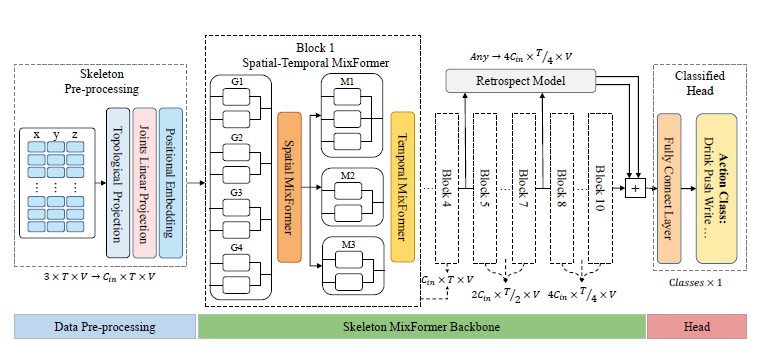
方法

符号表示

给定骨架图\(\mathcal{G}=(\mathcal{V},\mathcal{E})\)，其中\(\mathcal{V}=\left.(v_1,v_2,...,v_N)\right.\)表示N个顶点的关节集，\(\mathcal{E}\)表示由边构成的骨集。邻接矩阵为\(A\in\mathbb{R}^{N\times N}\)，并假设骨架图为无向图。假设骨架序列用\(X\)和\(A\)表示，则分层迭代和权重更新可由\(\mathcal{X}^{l+1}=\sigma(A\mathcal{X}^{l}W^{l})\)表示，其中\(W^l\in\mathbb{R}^{C_{l}\times C_{l+l}}\)表示第\(l\)层的权重矩阵。为了使邻接矩阵自适应，一些方法对输入进行卷积并使用自注意方法获得自适应相关邻接矩阵，如\(X^{l+1}=\sigma(f(X^{l})^{\mathrm{T}}M^{\mathrm{T}}Mf(\mathcal{X}^{l}))\)其中\(M\)和\(f(\cdot)\)分别表示可学习的矩阵和映射操作。

作者认为GNN中的相关矩阵的可解释性和Transformer中的权重关系举证的可解释性相对应，因此他们在Transformer使用完全可学习的相对位置嵌入（FL-RPE）而在GNN使用分组边缘掩码（G-EME）以提高性能。

Spatial MixFormer

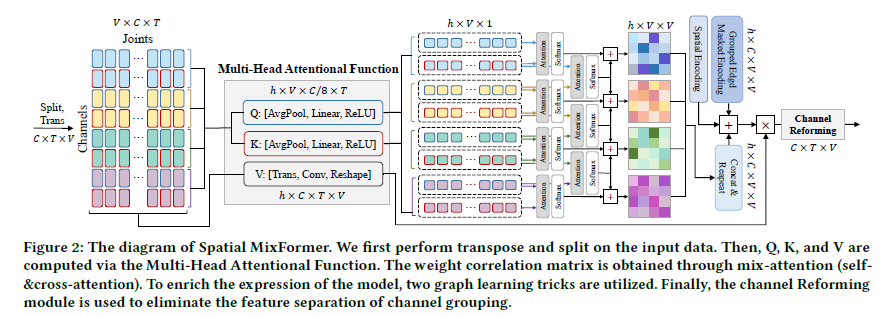
通道分组策略

与其在计算 𝑄 和 𝐾 时使维度翻倍再分割，不如直接利用原始通道数进行分割。这种方法减少了参数数量，同时保留了固有特征。
通过直接将输入分成 2𝑛 个单元组来增加分割通道组的数量，形成 𝑛 个组合组，从而捕捉多变量相互关联特征。如果将输入表示为\(\mathcal{X}_S^{in}\in\mathbb{R}^{C_s^{in}\times T\times V}\)，则分组过程可表示为 \[ \mathcal{X}'_S=split_n(trans_v(\mathcal{X}_S^{in}))=concat[x_s^1,x_s^2,...,x_s^n], \] 其中\(x_{s}^{i}\in\mathbb{R}^{V\times C_{s}^{in}/n\times T}\)。
为了最小化与Transformer结构相关的计算成本，直接将组中通道的数量汇总为一个，实现联合权重平滑化。接着应用全连接和线性激活，以确保在每个组内通过 𝑄 和 𝐾 获得的特征是全局的，同时保持每个组之间的邻接矩阵具有特定性，如下所示： \[ \begin{aligned}Q_i,K_i&=\sigma(linear(pool_a(split_2(x_s^i)))),\\A_s^i&=softmax(atten(Q_i,K_i)),\end{aligned} \] 其中\(Q_i,K_i \in \mathbb{R}^{V \times 1 \times 1}\)，\(pool_a(\cdot)\)为自适应平均池化，\(linear(\cdot)\)为全连接，\(\sigma(\cdot)\)为激活函数。
为了进一步增强多变量加权关联矩阵中所包含的信息容量，采用跨组注意力策略，并构建组间加权关联矩阵，具体步骤如下： \[ A_c^i=softmax(atten(Q_{i+1},K_i)), \] \[ A_{sc}^i=A_s^i+A_c^i+A_c^{i-1}, \] \[ A_{SC}=concat[A_{sc}^1,A_{sc}^2,...,A_{sc}^n], \] 其中第一个组不包含\(A_c^{i-1}\)，最后一个组不包含\(A_c^{i}\)。并利用空间编码（SE）和分组边缘屏蔽编码（G-EME）的邻接矩阵补充策略。\(A_{SE}\)有助于增强物理拓扑特性，确保模型的正确收敛方向，\(A_{G-EME}\)有助于增加关节之间权重学习的自主性和灵活性。因此，Spatial MixFormer 的最终权重关联矩阵\(A_{MF}\)可以表示为： \[ A_{MF}=A_{SC}+A_{SE}+A_{G-EME}, \] \[ A_{SE}=I{+}A_{in}+A_{out}, \] \[ A_{G-EME}=decoupling(A_m), \] 其中 \(A_{in},A_{out},A_m\) 分别代表向心邻接、离心邻接和参数化邻接。通过统一的计算得到\(V_S\)，并最终的空间输出可以表示如下： \[ V_S=Conv_{1\times1}(Trans_v(\mathcal{X}_S^{\prime})), \] \[ \mathcal{X}_{S}^{out}=\mathcal{X}_{S}^{in}+V_{S}A_{MF}. \]

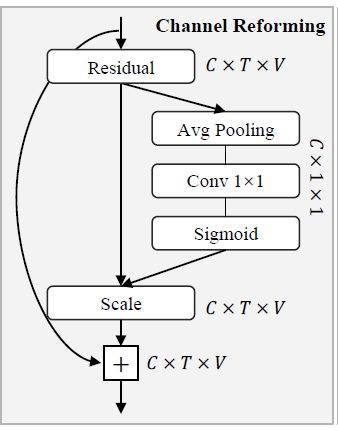
Channel Reforming Model

为了平滑组之间的特征分离并消除噪音，需要重新组织每个组的通道关系。对 SE-net进行了两项改进。首先，平均池化的对象是时间和通道，以关节作为基本维度。其次，移除了全连接层，确保在该模块中计算的关节之间的信息交互保持隔离，以保持纯净性。

Temporal MixFormer

Temporal MixFormer是多尺度卷积、时间Transformer和序列保持模块的mixer。为了保持三个子模块具有相同时间信息的输入连续性，在输入端没有采用通道分组策略。相反，通过\(1\times1\)的卷积降低通道维度以创建多个输入组。如果将这三个模块分别表示为M1、M2和M3，最终输出可以表示如下： \[ X_T^{out}=concat[X_T^{M1},X_T^{M2},X_T^{M3}] \]

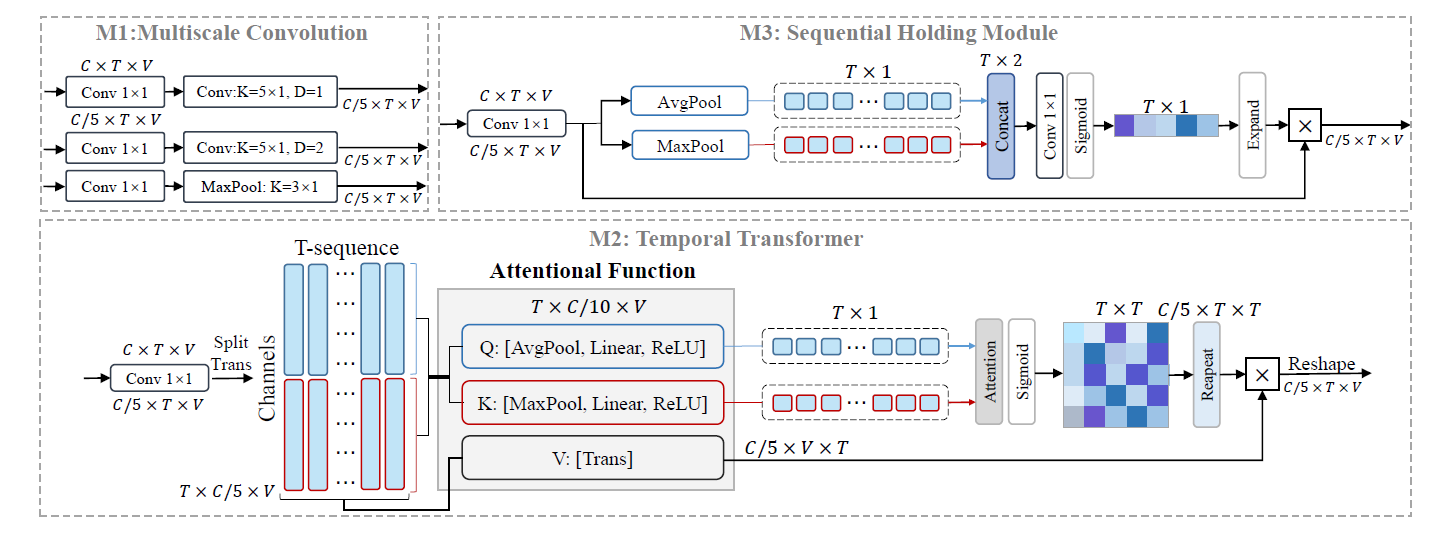
M1:多尺度卷积

MS-G3D采用一种固定滤波器和放松扩张率的策略，在时间域获取更多多变量多尺度信息，同时降低计算成本。当输入为\(X_{T}^{\overline{in}}\in \mathbb{R}^{Cin \times T\times V}\) ，这种策略可被表示为 \[ \begin{array}{c} X_{T}^{m 1}=\operatorname{Conv}_{c \rightarrow c / 5}\left(X_{T}^{i n}\right), \\ X_{T}^{M 1}=\operatorname{concat}\left[\left(X_{T}^{m 1}\right)_{1},\left(X_{T}^{m 1}\right)_{2},\left(X_{T}^{m 1}\right)_{3}\right], \end{array} \] 采用一种简单的优化方法，通过将原始加权替换为 2D-TCN的残差加权，以增强时间卷积中特征基线的灵活性。

M2:时间Transformer

相比于多尺度卷积，Transformer更好地获取全局时间信息，采用与 Spatial MixFormer 类似的压缩策略，但有三个关键区别：1) 关于组的数量，仅分为两个单元。2) 目标维度是时间，也就是说，通道和关节维度需要被压缩。3) 新的压缩方法，𝑄 和 𝐾 分别采用平均池化和最大池化。输入为\(X_{T}^{in}\)，时间Transformer可表示为 \[ \begin{array}{c} x_{t}^{1}, x_{t}^{2}=\operatorname{split}_{2}\left(\operatorname{trans}_{t}\left(\operatorname{Conv}_{c \rightarrow c / 5}\left(\mathcal{X}_{T}^{i n}\right)\right)\right), \\ Q_{t}=\sigma\left(\text { linear }\left(\operatorname{pool}_{a}\left(x_{t}^{1}\right)\right)\right), K_{t}=\sigma\left(\operatorname{linear}\left(\operatorname{pool}_{m}\left(x_{t}^{2}\right)\right)\right) \text {, } \\ A_{T}^{m 2}=\operatorname{sigmoid}\left(\operatorname{atten}\left(Q_{t}, K_{t}\right)\right), \\ \end{array} \] 其中\(x_{t}^{1}, x_{t}^{2} \in \mathbb{R}^{T \times C^{in}_t/10 \times V}\)，\(Q_t,K_t\in\mathbb{R}^{T\times1\times1}\)，\(pool_m(\cdot)\)为自适应最大池化。通过统一计算得到\(V_T\)，最终的空间输出可以表示如下： \[ \begin{array}{c}V_T=Conv_{1\times1}(Trans_t(\operatorname{Conv}_{c\to c/5}(\mathcal{X}_T^{in}))),\\ X_T^{\boldsymbol{M}2}=V_TA_T^{\boldsymbol{m}2},\end{array} \]

序列保持模块

在时间变换器模块中，获得\(Q\)代表时间特征的全局平均表示，以及 \(K\)代表具有突出动作表现的时间特征。在先前的模块中，\(Q\)和\(K\)通过矩阵乘法结合，获得差分时间邻接矩阵。在这个模块中，采用\(Q\)和\(K\)的线性组合，得到时间序列权重的第二个表示。顺序保持模块的目的是对原始的时间特征进行微调，这有利于识别具有大量类内差异的数据。相应的公式可以表示如下： \[ \begin{gathered} X_{T}^{\prime}=Trans_{t}(Conv_{c\rightarrow c/5}(\mathcal{X}_{T}^{in})), \\ A_{T}^{\prime}=Conv_{c\rightarrow c/2}(concat[pool_{a}(X_{T}^{\prime}),pool_{\boldsymbol{m}}(X_{T}^{\prime})]), \\ A_{T}^{\boldsymbol{m}3}=expand(sigmoid(A_{T}^{\prime})), \\ X_{T}^{M3}=X_{T}^{\prime}\cdot A_{T}^{m3}. \end{gathered} \]