SkeletonMAE
摘要
骨架序列表示学习通过其对人体关节和拓扑结构的建模能力,在动作识别中显示了巨大的优势。然而,当前的方法通常需要大量的标注数据来训练计算昂贵的模型。此外,这些方法忽略了如何利用骨架不同关节之间的细粒度依赖关系,来预训练一个可以泛化到不同数据集的高效骨架序列学习模型。在本文中,我们提出了一个高效的骨架序列学习框架,命名为骨架序列学习(SSL)。为了全面捕获人体姿态并获得有区分性的骨架序列表示,我们构建了一个基于非对称图的编码器-解码器预训练架构,命名为SkeletonMAE,它将骨架关节序列嵌入图卷积网络,并根据先验人体拓扑知识重构被屏蔽的骨架关节和边。然后,预训练的SkeletonMAE编码器与空间-时域表示学习(STRL)模块相结合,构建SSL框架。大量的实验结果显示,我们的SSL可以很好地泛化到不同的数据集,并在FineGym、Diving48、NTU 60和NTU 120数据集上优于目前最先进的自监督基于骨架的方法。此外,我们获得了可与一些完全监督方法相媲美的性能。
引言
论文背景: 骨架序列表示学习在动作识别中具有很大的优势,因为它能够有效地建模人体关节和拓扑结构。然而,现有的方法通常需要大量标记数据来训练计算成本高昂的模型,并且忽视了如何利用不同骨架关节之间的细粒度依赖关系来预训练一个能够在不同数据集上泛化良好的骨架序列学习模型。
过去方案: 以往的自监督骨架学习方法通常采用随机掩码策略来重构骨架,忽视了动作敏感的骨架区域。此外,这些方法通常擅长于链接预测和节点聚类,但在节点和图分类方面表现不佳。
论文的Motivation: 鉴于现有方法的局限性,本文旨在提出一种高效的骨架序列学习框架,通过预训练和空间-时间表示学习来充分利用骨架序列中的细粒度依赖关系,并在动作识别任务中取得更好的性能。
论文贡献: 1. SkeletonMAE的基于图的编码器-解码器预训练架构,将骨架关节序列嵌入到GCN中,并利用先验人体拓扑知识来引导被屏蔽的关节和拓扑结构的重建。 2. 为了学习骨架序列的全面时空依赖性,我们提出了一个高效的骨架序列学习框架,称为骨架序列学习(SSL),它将预训练的SkeletonMAE编码器与时空表示学习(STRL)模块集成。 3. 在FineGym、Diving48、NTU 60和NTU 120数据集上的大量实验结果表明,我们的SSL方法优于当前最先进的基于自监督的骨架动作识别方法,并达到可与最先进的完全监督方法媲美的性能。
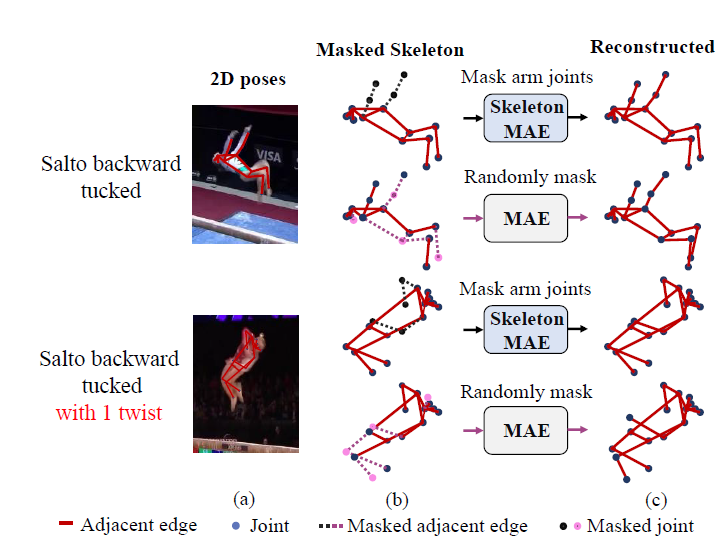
传统的MAE通常使用随机遮蔽策略来重构骨架,这往往会忽略对动作敏感的骨架区域。不同的是,SkeletonMAE基于先验人体拓扑知识重构被遮蔽的骨架关节和边缘,以获得对动作的全面感知。
方法

骨架序列预训练架构SkeletonMAE的详细信息如下:
构建了一个基于GIN的不对称编码器-解码器结构,用于重建关节特征,以增强动作表示能力。
基于GIN的编码器结构包含\(L_{D}\)个GIN神经网络层,用于在空间上学习关节表示。
解码器由一个GIN层组成,它使用来自编码器的隐藏特征作为输入,并重新构建原始输入的关节特征。
根据人体自然结构,将骨架序列中的关节分为不同的部分。
预训练SkeletonMAE
作者利用图同构网络(GIN)作为主干网络,提供更好的泛化偏置,更适合学习更泛化的自监督表示。
SkeletonMAE结构
构建了一个名为SkeletonMAE的基于非对称图的编码器-解码器预训练架构,将骨架序列及其先验拓扑知识嵌入到GIN中。SkeletonMAE遵循图的生成式自监督学习范式来实现。
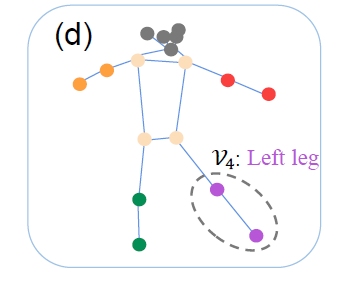
遵循Kinetics Skeleton数据集的joint label,如下图,根据身体的自然部位:\(\mathcal{V}_0,...,\mathcal{V}_5\),将所有的\(N = 17\)个关节点划分为\(R = 6\)个区域。然后,遮罩这些骨架区域,使SkeletonMAE能够基于相邻的关节重建遮罩的关节特征及其边缘。通过重建被遮罩的骨架关节和边缘,SkeletonMAE可以推断关节的底层拓扑结构,并获得对动作的全面感知。
SkeletonMAE是一种不对称的编码器-解码器架构,包括一个编码器和一个解码器。编码器由\(L_{D}\)个GIN层组成,将输入的2D骨架数据映射到隐藏特征上。解码器由仅包含一个GIN层的部分组成,在重建准则的监督下重新构建隐藏特征。根据先前的人体骨架知识,人体骨架可以表示为一个以关节为顶点、以肢体为边缘的图结构,将人体骨架表述为以下的图结构。
对包含\(N\)个人体骨架关节和\(T\)帧的二维坐标骨架序列进行如下预处理:
具体来说,我们将所有骨架关节及其拓扑结构嵌入到一个结构\(\mathcal{G}\)中,骨架结构和关节特征融合,得到关节序列矩阵\(\mathbf{S}\in \mathbb{R}^{N\times T \times2}\)。然后,将\(\mathbf{S}\)线性变换为\(\mathbf{S}\in \mathbb{R}^{N\times T\times D}\),其中\(D\)是可学习的参数,我们经验性地将\(T\)和\(D\)设置为64。
对于每个来自\(\mathbf{S}\)的骨架帧\(\mathbf{X}\in \mathbb{R}^{N\times D}\),我们用\(\mathcal{G} = (\mathcal{V},\mathbf{A},\mathbf{X})\)表示一个骨架,其中\(\mathcal{V}=\left\{v_{1}, v_{2}, \ldots \ldots, v_{N}\right\}\)是包含所有骨架关节的节点集合,\(N=|\mathcal{V}|\)是关节的数量,这里\(N=17\)。\(\mathbf{A} \in \left\{0,1\right \}^{N \times N}\)是一个邻接矩阵,其中\(\mathbf{A}_{i,j}=1\)表示关节\(i\)和\(j\)在物理上相连接,否则为0。节点\({v}_{i}\)的特征表示为\(\mathbf{x}{i}\in \mathbb{R}^{1 \times D}\)。\(\mathit{G}_{E}\)和\(\mathit{G}_{D}\)分别表示GIN编码器和GIN解码器。
骨骼关节掩蔽和重建
由于先前的人体骨架拓扑结构\(\mathbf{A}\)已经嵌入,并且明确了关节的聚合方式。受到GraphMAE的启发,该方法随机重建遮罩的图节点,SkeletonMAE基于先前的骨架拓扑结构来重建被遮罩的骨架特征\(\mathbf{X}\),而不是重建图结构\(\mathbf{A}\)或同时重建图结构\(\mathbf{A}\)和特征\(\mathbf{X}\)。
为了遮罩骨架关节特征,从\(\mathcal{V}=\left\{\mathcal{V}_0,...,\mathcal{V}_5 \right\}\)中随机选择一个或多个关节集合,其中包括一个子集\(\overline{\mathcal{V}}\subseteq \mathcal{V}\)用于遮罩。对于人体骨架序列,每个关节与其相邻的一些关节通信,以表示特定的动作类别。因此,不可能对所有动作类别遮罩所有关节集合。
然后,它们的特征都会被一个可学习的掩码标记向量\(\left[\boldsymbol{\mathbf{MASK}}\right ]=\mathbf{x}_{\left [ \boldsymbol{\mathbf{M}}\right ]} \in \mathbb{R}^{D}\)遮罩。因此,对于在被遮罩特征矩阵\(\overline{\mathbf{X}}\)中的\(\mathbf{v}_{i} \in \overline{\mathcal{V}}\)的遮罩关节特征\(\overline{\mathbf{x}}_{i}\)可以定义为,如果\(\mathbf{v}_{i} \in \overline{\mathcal{V}}\),则\(\overline{\mathbf{x}}_{i}=\mathbf{x}_{\left [ \boldsymbol{\mathbf{M}}\right ]}\),否则\(\overline{\mathbf{x}}_{i}= \mathbf{x}_{i}\)。我们将\(\overline{\mathbf{X}}\in \mathbb{R}^{N\times D}\)设置为SkeletonMAE的输入关节特征矩阵,\(\overline{\mathbf{X}}\)中的每个关节特征可以定义为\(\overline{\mathbf{x}}_{i}=\left \{ \mathbf{x}_{\left [ \boldsymbol{\mathbf{M}}\right ]}, \mathbf{x}_{i}\right \}\),\(i= 1,2,\cdots, N\)。因此,遮罩后的骨架序列可以表示为\(\overline{\mathcal{G}} =(\mathcal{V},\mathbf{A},\overline{\mathbf{X}})\),SkeletonMAE的目标是在给定部分观察到的关节特征\(\overline{\mathbf{X}}\)和输入邻接矩阵\(\mathbf{A}\)的情况下,重建\(\overline{\mathcal{V}}\)中的遮罩骨架特征。SkeletonMAE的重建过程可以被定义为: \[ \begin{equation} \left\{\begin{matrix}\mathbf{H}= \mathit{G}_{E}(\mathbf{A},\overline{\mathbf{X}}), \; \; \; \; \mathbf{H}\in \mathbb{R}^{N\times D_{h}} \\\mathbf{Y}= \mathit{G}_{D}(\mathbf{A},\mathbf{H}), \; \; \; \; \mathbf{Y}\in \mathbb{R}^{N\times D} \end{matrix}\right., \end{equation} \] 其中\(\mathbf{H}\)和\(\mathbf{Y}\)分别表示编码器输出和解码器输出。skeleton的目标可以形式化为最小化\(\mathbf{X}\)和\(\mathbf{Y}\)之间的分歧。
重建标准
为了使重建准则专注于不平衡的难-易样本中的较难样本,SkeletonMAE采用Re-weighted Cosine Error (RCE),即可以通过缩放余弦误差\(\beta\geq1\)的幂来降低简单样本在训练中的贡献,而对于高置信度的预测,它们对应的余弦误差通常小于1,并且在缩放因子\(\beta>1\)时更快地衰减为零。给定原始特征\({\mathbf{X}}\in \mathbb{R}^{N\times D}\)和重建输出\(\mathbf{Y}\in \mathbb{R}^{N\times D}\),RCE的定义如下: \[ \begin{equation} \mathcal{L}_{\textrm{RCE}}=\sum_{\mathbf{v}_{i} \in \overline{\mathcal{V}}}^{}(\frac{1}{ |\overline{\mathcal{V}}|}-\frac{\mathbf{x}_{i}^\mathrm{T}\cdot\mathbf{z}_{i}}{\left |\overline{\mathcal{V}}|\times \| \mathbf{x}_{i}\right \| \times \left \| \mathbf{z}_{i}\right \|})^{\beta }, \end{equation} \] 这个公式表示在所有被遮罩的关节上,重建特征与输入特征之间的相似性差距的平均值。\(\beta\)被设置为2,即采用了平方的幂来缩放余弦误差的贡献,以便更强调容易样本的影响。
Fine-tuning
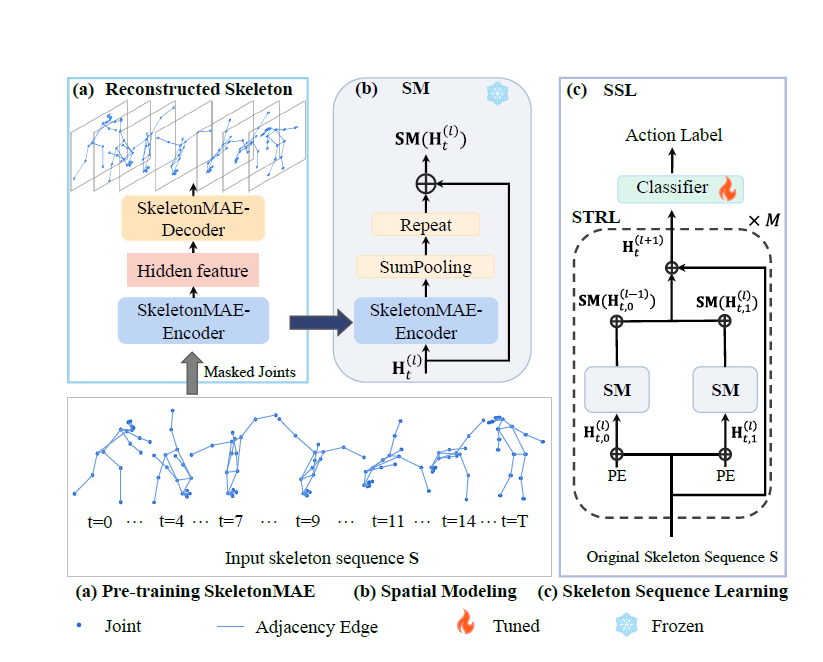
如上图,骨架序列学习(SSL)的流程如下:
在预训练阶段,我们构建一个名为SkeletonMAE的编码器-解码器模块,将骨架关节及其先前的拓扑知识嵌入到GIN中,并重建底层的遮罩关节和拓扑结构。
SM包含了经过预训练的SkeletonMAE编码器。
我们将SM结构整合起来构建了\(M\)层的时空表示学习(STRL)模型,然后进行端到端的微调。
Spatial-Temporal Representation Learning
STRL包含两个经过预训练的SkeletonMAE编码器,用于空间建模(SM)。SM的输入是骨架序列\(\mathbf{S}\),其输出通过\(1\times1\)卷积与输入连接,以进行残差连接。
如(c)所示,首先将输入的骨架序列\(\mathbf{S}\in \mathbb{R}^{N\times T \times D}\)与可学习的时间位置嵌入\(\textrm{PE}\)相加,以获得骨架序列特征\(\mathbf{H}_{t}^{(\mathit{l})}\in \mathbb{R}^{P\times N\times {D}^{(\mathit{l})}}\)。为了建模多个人体骨架之间的交互,我们从\(\mathbf{H}_{t}^{(\mathit{l})}\)中获取两个独立的特征(\(P=2\)),分别用于两个人的特征表示,即\(\mathbf{H}_{t,0}^{(\mathit{l})}\in \mathbb{R}^{N \times {D}^{(\mathit{l})}}\)和\(\mathbf{H}_{t,1}^{(\mathit{l})}\in \mathbb{R}^{N \times {D}^{(\mathit{l})}}\)。然后,我们将关节表示\(\mathbf{H}_{t,0}^{(\mathit{l})}\)和关节的先验知识\(\widetilde{\mathbf{A}}\)传递给SM模块, \[ \begin{equation} \begin{split} \textrm{SM}(\mathbf{H}_{t,0}^{(\mathit{l})})=\textrm{Repeat}(\textrm{SP}(\mathit{G}_{E}\left (\widetilde{\mathbf{A}}, \mathbf{H}_{t,0}^{(\mathit{l})} \right));N)\oplus \mathbf{H}_{t,0}^{(\mathit{l})}, \end{split} \end{equation} \] 在这里,\({G}_{E}\)是SkeletonMAE的编码器,\(\textrm{SP}(\cdot{})\)表示求和池化,\(\textrm{Repeat} (\cdot{};N)\)表示在求和池化后将单个关节重复成\(N\)个关节表示,并将其与\(\mathbf{H}_{t,0}^{(\mathit{l})}\)残差连接以获得全局关节表示\(\textrm{SM}(\mathbf{H}_{t,0}^{(\mathit{l})})\)。通过这种方式,SM模块可以通过单个关节表示获取全局信息,并通过所有关节表示来约束一些关节特征。类似地,通过相同的方式获得了\(\textrm{SM}(\mathbf{H}_{t,1}^{(\mathit{l})})\)。如(c)所示,我们得到了包含第0个人和第1个人之间动作交互的关节特征\(\textrm{SM}(\mathbf{H}_{t}^{(\mathit{l})})\)。根据图卷积的更新规则,我们可以在多层GCN中从\(\mathbf{H}_{t}^{(\mathit{l})}\)得到\(\mathbf{H}_{t}^{(\mathit{l}+1)}\)。最终的骨架序列表示如下定义: \[ \begin{equation} \mathbf{H}_{t}^{(\mathit{l}+1)}=\sigma\left ( \textrm{SM}(\mathbf{H}_{t}^{(\mathit{l})}) \mathbf{W}^{(\mathit{l})}\right ). \end{equation} \]
其中\(\mathbf{W}^{(\mathit{l})}\)表示第\(l\)层的可训练权重矩阵,\(\sigma(\cdot)\)表示ReLU激活函数。 接着采用了多尺度时间池化(multi-scale temporal pooling)来获得最终的输出。最后,由MLP和softmax组成的分类器预测动作类别。