Hypergraph Transformer

Posted on 2023-08-22 Edited on 2024-03-06 In 骨架动作识别

摘要

骨架基础的动作识别旨在给定人体关节坐标及其骨架互连来识别人类动作。通过将关节定义为顶点，其自然连接定义为边，先前的工作成功地采用了图卷积网络(GCN)来建模关节的共现，并获得了出色的性能。更近期，发现了GCN的一个限制，即拓扑结构在训练后是固定的。为了放松这种限制，采用了自注意力(SA)机制使GCN的拓扑结构对输入变得自适应，产生了目前最好的混合模型。同时，也尝试了简单的Transformer，但由于缺乏结构先验，它们仍落后于目前最好的基于GCN的方法。与混合模型不同，我们提出了一种更优雅的方法，通过图距离嵌入将骨连接性结构融入Transformer。我们的嵌入在训练期间保留了骨架结构的信息，而GCN仅将其用于初始化。更重要的是，我们揭示了图模型通常存在的一个潜在问题，即成对聚合从本质上忽略了身体关节之间的高阶运动依赖性。为弥补这一空白，我们在超图上提出了一种新的自注意力(SA)机制，称为超图自注意力(HyperSA)，以融入内在的高阶关系。我们将结果模型称为Hyperformer，它在NTU RGB+D、NTU RGB+D 120和Northwestern-UCLA数据集上都优于目前最好的图模型，在精度和效率方面。

引言

论文背景: 骨骼动作识别是一项重要的研究领域，通过使用骨骼关节坐标来识别人类动作。过去的研究主要采用图卷积网络（GCNs）来建模关节之间的关联，并取得了较好的性能。然而，GCNs存在拓扑结构固定的限制，无法灵活适应输入数据。为了解决这个问题，本研究引入了自注意机制，使得GCNs的拓扑结构能够根据输入数据自适应调整，从而提高了模型的性能。

过去方案: 过去的研究主要采用图卷积网络（GCNs）来建模关节之间的关联，并取得了较好的性能。然而，GCNs存在拓扑结构固定的限制，无法灵活适应输入数据。为了解决这个问题，一些研究尝试使用Transformer模型，但由于缺乏结构先验知识，其性能仍然落后于GCN-based方法。

论文的Motivation: 鉴于GCNs和Transformer模型在骨骼动作识别中的局限性，本研究旨在提出一种更优雅的解决方案，将骨骼关联信息引入Transformer模型中。通过引入基于图距离的相对位置嵌入和超图自注意机制，该模型能够更好地捕捉骨骼关节之间的高阶关系，并在准确性和效率方面超越现有的图模型。

论文的Contribution： 1. 提出通过基于图距离的相对位置嵌入将人体骨架的结构信息融入Transformer，利用了Transformer与目前最先进的混合模型之间的差距 2. 基于超图表示设计了一种新的自注意力(SA)变体，称为超图自注意力(HyperSA)。据作者所知，他们的工作是第一种将超图表示应用于基于骨架的动作识别的工作，它考虑了成对和高阶关节关系，超越了当前最先进的方法（并不是第一种） 3. 根据所提出的相对位置嵌入和HyperSA构建了一个轻量级的Transformer。它在基于骨架的动作识别基准测试中优于目前最好的图模型，无论是效率还是准确率方面。

在latex源码，作者在引言第三段“This can be attributed to the fact that the formulation of the vanilla Transformer ignores the unique characteristics of skeleton data， i.e.，” 注释掉了一部分原有的内容，注释者认为“对应这个问题的改动很小”，注释内容翻译如下：

Transformer假设输入标记是同质的，然而人体关节本质上是异质的，例如，每个物理关节发挥独特的作用，因此与其他关节有不同的关系。这些固有关系在不同的动作中持续存在，与输入的关节坐标或动作类别无关。骨连接性:Transformer依赖排列不变的注意力操作，这会忽略位置信息。普通的注意力操作假设排列不变性，因此破坏了位置信息。为了缓解这个问题，绝对位置嵌入被广泛使用。然而，它们无法表示人体关节之间复杂的骨连接关系。与绝对位置嵌入相比，相对位置嵌入被证明在语言、视觉和图数据等各种任务上的Transformer中更优越，因为它们保留了比前者更多的结构信息。

Preliminaries

自注意力

给定输入序列$X=(\vec{x}_1，...，\vec{x}_n)$，每个标记$\vec{x}_i$先被映射到关键表示 $\vec{k}_i$ ，查询表示 $\vec{q}_i$ 和值表示 $\vec{v}_i$。然后通过$\vec{q}_i$ 和 $\vec{k}j$ 的点乘经softmax函数计算出两个标记间的注意力分数$A{ij}$: \[ \begin{equation} A_{ij} = \vec{q}_i \cdot \vec{k}_j^\top， \end{equation} \] 每个位置的最终输出是所有值表示的加权和: \[ \begin{equation} \vec{y}_i = \sum_{j=1}^n A_{ij}\vec{v}_j \end{equation} \] 多头自注意力(Multi-Head Self-Attention， MHSA)是Transformer的常用扩展，分成多个子空间进行自注意力的计算。

超图表示

与标准图边不同，超图中的超边连接两个或多个顶点。一个无权超图定义为$\mathcal{H} = (\mathcal{V}， \mathcal{E})$，由顶点集$\mathcal{V}$和超边集$\mathcal{E}$组成。超图$\mathcal{H}$可以用一个$|\mathcal{V}| \times |\mathcal{E}|$ 的关联矩阵$H$表示，其中的元素定义如下:

$$ \[\begin{equation} h_{v， e}=\left\{ \begin{aligned} 1， \quad if \quad v \in e\\ 0， \quad if \quad v \notin e\\ \end{aligned}\right . \end{equation}\] $$

顶点$v \in \mathcal{V}$的度定义为$d(v) = \sum_{e \in \mathcal{E}} h_{v， e}$，超边$e \in \mathcal{E}$的度定义为$d(e) = \sum_{v \in \mathcal{V}} h_{v， e}$。度矩阵$D_e$和$D_v$分别将所有超边的度和所有顶点的度设为对角元素。

在本工作中，考虑所有顶点$d(v)=1$的特殊情况，即身体关节被划分为$\vert \mathcal{E} \vert$个不相交的子集，这在实践中很高效。值得注意的是，在这种情况下，关联矩阵$H$等效于一个分割矩阵。每行是一个one hot向量，表示每个关节所属的组。

方法

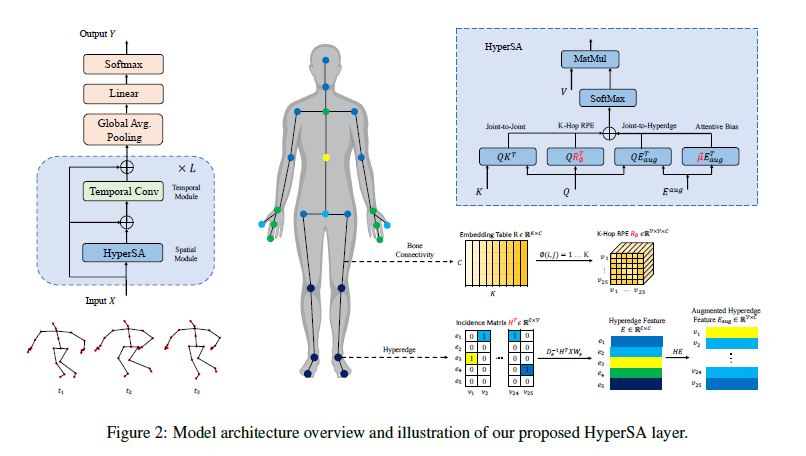
派生超边特征

给定一个关联矩阵$H$，作者提出了一种有效的方法来获得连接到每个超边的关节子集的特征表示。令$C$表示特征维数，每个关节的特征$X \in \mathbb{R}^{\vert \mathcal{V} \vert \times C}$ 首先通过以下规则聚合为子集表示$E \in \mathbb{R}^{\vert \mathcal{E} \vert \times C}$: \[ \begin{equation} E = D_e^{-1}H^\top XW_{e}， \end{equation} \]

其中: 1. 关联矩阵$H$与输入$X$的乘积本质上是将每个子集中属于该子集的关节特征求和。 2. 超边的度矩阵的逆用于归一化的目的。 3. 投影矩阵$W_{e} \in \mathbb{R}^{C\times C}$进一步转换每个超边的特征以获得它们的最终表示。

然后通过将超边表示分配给每个关联关节的位置，构造增强的超边表示$E_{aug} \in \mathbb{R}^{\vert \mathcal{V} \vert \times C}$:

\[ \begin{equation} E_{aug} = HD_e^{-1}H^\top XW_{e}. \end{equation} \]

人体骨骼结构编码

人体骨骼构成了一个机械系统，关节之间的连接关系会对运动产生重要影响。因此有必要在Transformer中融入骨骼的结构信息。

参考图像和语言领域Transformer中的相对位置编码设计，作者提出了 k跳相对位置编码（k-Hop Relative Positional Embedding）：$R_{ij} \in \mathbb{R}^C$，它通过第i个和第j个关节之间的最短路径距离(SPD)从一个可学习的参数表中索引，这样可以将骨骼结构知识注入到Transformer中。

超图自注意力机制

基于获得的超边表示和骨骼拓扑编码，定义超图自注意力如下: $$ \[\begin{align} \begin{split} A_{ij} = & \underbrace{\vec{q}_i \cdot \vec{k}_j^\top}_{\text{(a)}} + \underbrace{\vec{q}_i \cdot E_{aug， j}^\top}_{\text{(b)}} \\ & + \underbrace{\vec{q}_i \cdot R_{\phi(i， j)}^\top}_{(c)} + \underbrace{\vec{u} \cdot E_{aug， j}^\top}_{(d)}， \end{split} \end{align}\] $$ 其中$\vec{u} \in \mathbb{R}^{C}$是一个与查询位置无关的可学习的静态键。

各项表示:

(a)仅是普通的自注意力，表示关节对关节的注意力。 (b)计算第i个查询和第j个键对应的超边之间的关节对超边的注意力。 (c)通过k跳相对位置编码注入人体骨骼的结构信息。 (d)目的是计算不同超边的注意力偏差，与查询位置无关。它为连接到某个超边的每个关节赋予相同数量的注意力。

注意(a)和(b)项可以通过分配律组合，仅需要额外的矩阵加法步骤。此外，(d)项的复杂度为$O(\vert \mathcal{V} \vert C^2)$，与(a)项相比计算量可以忽略不计。

关系偏差

Transformer假设输入标记是同质的，而人体关节本质上是异质的，例如每个物理关节发挥独特的作用，因此与其他关节有不同的关系。

为考虑骨架数据的异质性，将每对关节的固有关系表示为一个可训练的标量参数$B_{ij}$，称为关系偏差(RB)。在聚合全局信息之前，将其添加到注意力分数中: \[ \begin{equation} \vec{y}_i = \sum_{j=1}^n (A_{ij} + B_{ij}) \vec{v}_j \end{equation} \]

划分策略

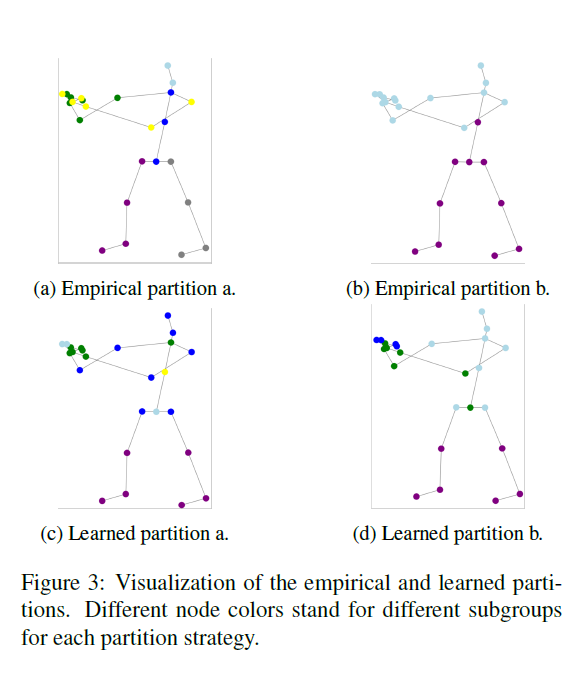
作者在实验中发现，使用经验划分的Hyperformer可以达到优异的性能。但是，找到最佳的经验划分策略需要大量体力工作，并且最佳划分策略会受限于拥有固定数目关节的特定骨架。因此作者提供了一种方法来自动化搜索有效划分策略的过程。

为了使划分矩阵可学习，通过沿其列轴应用softmax将二元划分矩阵参数化并松弛为连续版本:

\[ \tilde{H}=\left\{\tilde{h}_{v e}=\frac{\exp \left(h_{v e}\right)}{\sum_{e=1}^{|\mathcal{E}|} \exp \left(h_{v e}\right)} ; i=1 \ldots|\mathcal{V}|, j=1 \ldots|\mathcal{E}|\right\} \]

这样寻找最优离散分割矩阵H的问题就转化为学习一个最优的连续分割矩阵$\tilde{H}$了，它可以与Transformer的参数联合优化。

在优化结束时，可以通过对$\tilde{H}$的每行应用argmax操作来获得一个离散的分割矩阵: \[ \begin{equation} H = \mathrm{argmax}(\tilde{H}) \end{equation} \] 注意，通过变化$\tilde{H}$的初始化，可以轻松获得许多不同的划分提议。实验表明，所有这些提议都证明是合理的。有趣的是，所有学习到的提议都是对称的，如图所示，这表明对称性是固有关节关系的一个重要方面。

模型架构

空间建模

在多头HyperSA之前应用层规范化(LN)，并在输出添加残差连接，遵循标准的Transformer架构。

在前馈层中，Transformers针对每个token都进行了一个独立的多层感知机(MLP)操作，这个MLP试图捕获每个token内部的复杂特征表示，对于一些复杂的token如图像patch或词嵌入，增强其内部表示确实很重要。但是对于骨架动作识别任务中的简单三维关节坐标来说，这个额外的MLP是不必要的。因为动作识别更依赖于token之间的关系，即关节间的共现模式。所以文章建议可以移除MLP层，以减少计算和内存需求，这可以使基于Transformer的模型更轻量和高效。

为了引入非线性，在每个空间和时序建模模块块之后添加了一个ReLU层。

时序建模

为了建模人体姿态的时序相关性，最终模型中采用了多尺度时序卷积(MS-TC)模块。该模块包含三个卷积分支，先进行1×1卷积减少通道维度，然后是不同组合的核大小和扩张率。最后把卷积分支的输出拼接在一起。

Hyperformer通过交替堆叠HyperSA和时序卷积层构建,如下:

\[ \begin{align} & z^{(l)} = \text{HyperSA}(LN(z^{(l-1)})) + z^{(l-1)} \\ & z^{(l)} = \text{TemporalConv}(LN(z^{(l)})) + z^{(l-1)} \\ & z^{(l)} = \text{ReLU}(z^{(l)}) \end{align} \]