Video Test-Time Adaptation for Action Recognition
摘要
尽管在同一分布的测试数据上评估时,动作识别系统可以达到最佳性能,但它们对于测试数据中的意外分布变化很容易受到攻击。然而,迄今为止尚未展示视频动作识别模型的测试时间自适应能力。我们提出了一种针对时空模型的方法,可以在单个视频样本的每一步上进行自适应。该方法通过一种特征分布对齐技术,将在线估计的测试集统计数据与训练统计数据进行对齐。我们进一步通过对同一测试视频样本进行时间增强视图的预测一致性来强化。在三个基准动作识别数据集上的评估结果表明,我们提出的技术不依赖于具体的架构,能够显著提高最先进的卷积架构TANet和Video Swin Transformer的性能。我们的方法在单个分布变化的评估和随机分布变化的挑战性情况下都表现出了显著的性能提升。
背景信息:
论文背景: 行为识别系统在对分布内的测试数据进行评估时可以达到最佳性能,但对于测试数据中的未预期分布变化却很脆弱。例如,用于识别机动或行人交通事件的摄像头可能会记录罕见的天气状况,如冰雹;体育运动识别系统可能会受到体育场馆观众产生的干扰的影响,如照明弹的烟雾。然而,迄今为止,尚未展示出针对常见分布变化的视频行为识别模型的测试时间自适应方法。
过去方案: 图像分类中的分布变化可以通过测试时间自适应(TTA)来缓解,使用未标记的测试数据来调整模型以适应数据分布的变化。但这些方法不适用于行为识别。大多数行为识别应用需要在线运行内存和计算资源消耗大的时间模型,并且需要在硬件限制下实现最小延迟。此外,视频比图像更容易受到分布变化的影响。现有的TTA算法在处理视频数据时效果不佳。
论文的Motivation: 鉴于现有方法的局限性,本文旨在提出一种在线测试时间自适应的行为识别方法,能够适应测试数据中的分布变化,并且适用于不同的行为识别模型。通过特征对齐技术和预测一致性约束,本文的方法能够在单个视频样本上进行自适应,显著提高行为识别性能。
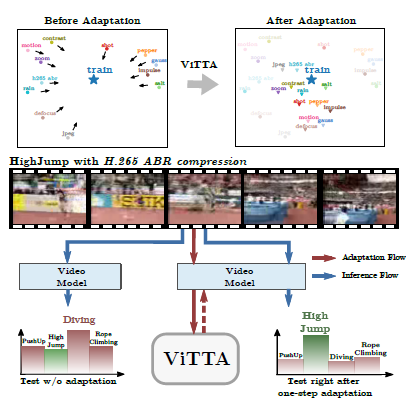
方法
优化目的:
给定一个在视频序列训练集\(S\)训练好的多层神经网络\(\phi\)以及网络的最优参数\(\hat{\theta}\)。在测试的时候,该网络被用于未标签的测试集\(T\),而\(T\)可能与\(S\)中的数据分布不同。该方法的目的是为了能使得网络\(\phi\)能够适应这种分布变化,以最大限度地提高在测试视频数据集上的性能。
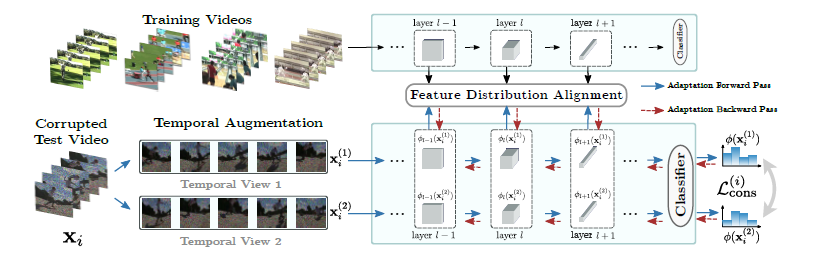
特征分布对齐
论文通过对齐为训练和测试视频计算的特征映射的分布来执行自适应。根据最近对TTA的研究,采用均衡特征映射的均值和方差的方法做到对齐分布。用\(\phi_{l}(\mathbf{x}; \theta)\)表示网络\(\phi\)的第\(l\)层对视频\(\mathbf{x}\)计算得到的特征图,其中\(\mathbf{\theta}\)是用于计算的参数向量。该特征图是一个尺寸为\(({c_l},t_l,h_l,w_l)\)的张量,其中\(c_l\)表示第\(l\)层的通道数,\(t_l\)、\(h_l\)和\(w_l\)分别表示其时间和空间维度。用\(V={[1,t_l]\times[1,h_l]\times[1,w_l]}\)表示特征图的时空范围,并用\(\phi_{l}(\mathbf{x};\mathbf{\theta})[v]\)表示特征图中体素\(v \in V\)上的一个\(c_l\)元素特征向量。 数据集\(D\)中第\(l\)层特征的均值向量可以计算为样本期望值: \[ \begin{equation} \mu_{l} (D;\mathbf{\theta}) = \mathbb{E}_{\substack{\mathbf{x} \in D\\ v \in V}} \big[ \phi_{l} (\mathbf{x};\mathbf{\theta})[v] \big] , \end{equation} \] 第\(l\)层特征的方差向量可以计算为: \[ \begin{equation} {\sigma^2}_{l} (D;\mathbf{\theta}) = \mathbb{E}_{\substack{\mathbf{x} \in D\\ v \in V}} \left[ \big( \phi_{l} (\mathbf{x};\mathbf{\theta})[v] - \mu_{l} (D;\mathbf{\theta}) \big)^2 \right] \end{equation} \] 为了简化方程的表达,将训练统计量的符号表示缩短为\({\hat{\mu}}_l=\mu_{l}(\mathit{S};\hat{\mathbf{\theta}})\)和\(\hat{\sigma}^2_l={\sigma^2}_l(\mathit{S};\hat{\mathbf{\theta}})\)。在论文的实验中,在训练数据上预先计算样本期望和方差。当这些数据不再可用时,它们可以被另一个未标记数据集的统计数据所取代,该数据集已知是由类似分布生成的。对于具有批归一化层的网络,可以使用这些层中累积的运行均值和方差来代替计算训练集的统计量,虽然会有轻微的性能损失。
总体方法是通过迭代更新参数向量\(\mathbf{\theta}\),以使选定层的测试统计与计算的训练数据统计相一致。这可以形式化为最小化对齐目标 \[ \begin{equation} \mathcal{L}_{\text {align }}(\theta)=\sum_{l \in L}\left|\mu_{l}(T ; \theta)-\hat{\mu}_{l}\right|+\left|\sigma_{l}^{2}(T ; \theta)-\hat{\sigma}_{l}^{2}\right| \end{equation} \] 关于参数向量\(\mathbf{\theta}\)的最小化问题,其中\(L\)是要对齐的层的集合,\(|\cdot|\)表示向量的\(l_1\)范数,\(\mathit{T}\)表示测试集。论文的方法是通过训练网络来对齐分布,与基于特征对齐的TTA技术在思路上有所不同,后者仅调整归一化层中训练期间累积的运行统计量,因此在测试时并没有真正学习。更新整个参数向量的事实使该方法与仅更新仿射变换层参数的现有算法有所区别,并且在自适应过程中更具灵活性。即使方法调整了完整的参数向量,在持续自适应实验中发现,论文的方法可以快速适应周期性的分布变化。当测试数据流中的分布变化被移除时,网络可以迅速恢复到原始性能。论文还发现,对于TANet和Video Swin Transformer这两种架构,通过对齐四个块中的最后两个块的特征分布可以实现最佳性能。因此,论文将\(L\)设置为包含这两个块中的层。
在线自适应
在公式(3)中优化目标需要迭代估计测试集的统计量。在在线视频识别系统中,通常需要以最小的延迟处理数据流,因此这是不可行的。因此,需要将特征对齐方法适应到在线场景中。假设测试数据以视频序列的形式逐步展示给自适应算法,表示为\(\mathbf{x}\),其中\(i\)是测试视频的索引。对序列中的每个元素执行一步自适应。单个测试样本上计算的特征统计量不能代表整个测试集上的特征分布,因此不能仅仅依靠它们来对齐分布。因此,通过对连续测试视频上计算的统计量进行指数移动平均来近似测试集的统计量,并将其用于对齐。定义第\(i\)次迭代中的均值估计为: \[ \begin{equation} {\mu_{l}}^{(i)}(\mathbf{\theta})=\alpha\cdot \mu_{l}(\mathbf{x}_i;\mathbf{\theta}) + (1-\alpha)\cdot {\mu_{l}}^{(i-1)}(\mathbf{\theta}) \end{equation} \] 其中,\(1-\alpha\)是动量项,通常设置为常见的选择\(0.9\)(\(\alpha=0.1\))。 类似地,定义第\(i\)次迭代中的方差估计为: \[ \begin{equation} {\sigma^2_{l}}^{(i)}(\mathbf{\theta})=\alpha\cdot \sigma^2_{l}(\mathbf{x}_i;\mathbf{\theta}) + (1-\alpha)\cdot {\sigma^2_{l}}^{(i-1)}(\mathbf{\theta}). \end{equation} \] 为了适应在线自适应,第\(i\)次对齐迭代中的目标函数被近似为: \[ \begin{equation} \mathcal{L}^{(i)}_\mathrm{align}(\mathbf{\theta})=\sum_{l \in ls} \lvert {\mu_{l}}^{(i)}(\mathbf{\theta}) - \hat{\mu}_l \rvert + \lvert {\sigma^2_{l}}^{(i)}(\mathbf{\theta}) - \hat{\sigma}^2_l \rvert \end{equation} \] 这种方法同时减小了估计量的方差,并让网络持续适应测试数据分布的变化。
时序增强
为了进一步提高该方法的有效性,利用数据的时间性质创建了相同视频的\(M\)个重新采样视图。论文用\(\mathbf{x}^{(m)}_i\)表示输入视频的时间增强视图,其中\(1\le m \le M\)。 论文计算视频\(\mathbf{x}_i\)在这\(M\)个视图上的均值和方差向量,以提高单个视频上的统计量的准确性: \[ \begin{equation} \mu_{l} (\mathbf{x}_i;\mathbf{\theta}) = \mathbb{E}_{\substack{m \in M\\ v \in V}} \big[ \phi_{l} (\mathbf{x}^{(m)}_i;\mathbf{\theta})[v] \big] , \end{equation} \] \[ \begin{equation} \sigma^2_{l} (\mathbf{x}_i;\mathbf{\theta}) = \mathbb{E}_{\substack{m \in M\\ v \in V}} \left[ \big( \phi_{l} (\mathbf{x}^{(m)}_i;\mathbf{\theta})[v] - \mu_{l} (\mathbf{x}_i;\mathbf{\theta}) \big)^2 \right] . \end{equation} \] 在第\(i\)次迭代中,\(\mu_{l} (\mathbf{x}_i;\mathbf{\theta})\)和\(\sigma^2_{l} (\mathbf{x}_i;\mathbf{\theta})\)用于计算迭代\(i\)中的均值和方差估计值。
此外,论文要求\(M\)个视图之间的相应预测具有一致性。 论文通过对网络对输入视图进行预测的类别概率进行平均来建立伪标签,即\(y(\mathbf{x})=\frac{1}{M} \sum_{m=1}^{M} \phi(\mathbf{x}^{(m)}_i;\mathbf{\theta})\),并定义第\(i\)次迭代中的一致性目标为 \[ \begin{equation} \mathcal{L}^{(i)}_\mathrm{cons} (\mathbf{\theta})= \sum_{m=1}^{M} \lvert \phi (\mathbf{x}^{(m)}_i;\mathbf{\theta}) - y(\mathbf{x}) \rvert. \end{equation} \] 在第\(i\)次对齐迭代中,论文通过以下梯度更新网络参数: \[ \begin{equation} \min_{\mathbf{\theta}} \mathcal{L}^{(i)}_\mathrm{align}(\mathbf{\theta}) + \lambda\cdot \mathcal{L}^{(i)}_\mathrm{cons} (\mathbf{\theta}), \end{equation} \] 其中\(\lambda\)是系数,论文将其设置为0.1。在消融研究中,论文展示了将\(M=2\)设定为足以显著提升性能的方法,以及均匀等距重新采样输入视频可以获得最佳结果。