MViT
摘要
我们提出了用于视频和图像识别的多尺度视觉Transformer(MViT),通过将多尺度特征层次结构的开创性想法与Transformer模型相连接。多尺度Transformer具有多个通道-分辨率尺度阶段。从输入分辨率和小通道维度开始,这些阶段在减小空间分辨率的同时分层扩展通道容量。这创建了一个多尺度特征金字塔,早期层以高空间分辨率操作,以模拟简单的低层次视觉信息,而深层以空间粗糙但复杂的高维特征操作。我们评估了这个基本的架构先验来模拟视觉信号的密集性质,针对多种视频识别任务进行了评估,其中它的表现优于依赖于大规模外部预训练的并且计算和参数成本高5-10倍的同时期视觉Transformer。我们进一步去除了时间维度,并将我们的模型应用于图像分类,其中它比视觉Transformer之前的工作中表现更好。
方法
通用多尺度变压器架构是建立在stages得核心概念上的。每一个stage由多个具有特定时空分辨率和channel维度的Transformer块组成。主要思想是逐步扩大信道容量,同时汇集网络从输入到输出的分辨率。
多头池化注意力
多头池化注意力(Multi Head Pooling
Attention,MHPA)是一种可以在Transformer块中灵活建模不同分辨率的自注意力算子,使得多尺度Transformer可以在不断变化的时空分辨率下运行。与原始的多头注意力算子相比,MHPA将潜在张量序列进行池化,以减少参与输入的序列长度(分辨率),如下图。
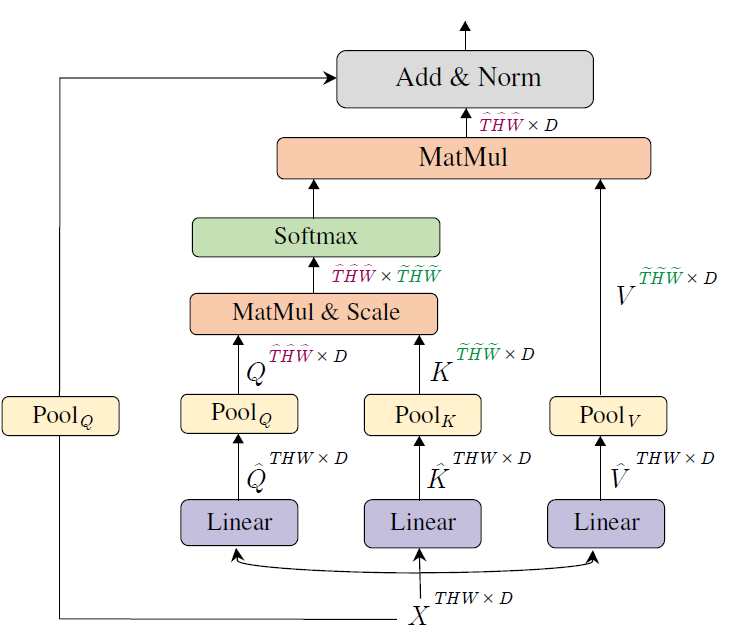 输入\(X \in
\mathbb{R}^{L \times D}\)是一个序列长度为\(L\)的\(D\)维输入张量,与MHA一样得到query、key、value:
输入\(X \in
\mathbb{R}^{L \times D}\)是一个序列长度为\(L\)的\(D\)维输入张量,与MHA一样得到query、key、value:
\[ \hat{Q} = XW_{Q} \quad \hat{K} = XW_{K} \quad \hat{V} = XW_{V} \]
池化算子:\(\mathcal{P}(\cdot ; \mathbf{\Theta})\)沿着每个维度对输入张量执行池化核计算。\(\mathbf{\Theta}\)内的参数为\(\mathbf{\Theta} := (\mathbf{k}, \mathbf{s}, \mathbf{p})\),分别对应池化核大小、步长、padding。因此注意力机制的计算会变为:
\[ \operatorname{PA}(\cdot) = \operatorname{Softmax}(\mathcal{P}(Q; \mathbf{\Theta}_Q)\mathcal{P}(K; \mathbf{\Theta}_K)^T/\sqrt{d})\mathcal{P}(V; \mathbf{\Theta}_V), \]
计算复杂度:用\(f_Q\),\(f_K\)和\(f_V\)表示序列长度缩小因子有,
\[ f_j = s^j_T \cdot s^j_H \cdot s^j_W, \ \forall \ j \in \{Q,K,V\}. \]
考虑将\(\mathcal{P}(; \Theta)\)的输入张量的维度表示为\(D \times T \times H \times W\),每个MHPA头部的运行时复杂度为\(O(THW D/h (D+THW/f_Qf_K))\),存储复杂度为\(O(THWh(D/h + THW/f_Qf_K))\)。
多尺度Transformer网络
ViT
Vision Transformer(ViT)架构通过将分辨率为\(T\times H \times W\)的输入视频分成大小为\(1\times 16 \times 16\)的不重叠补丁,并对展平的图像补丁应用逐点线性层,将它们投影到Transformer的潜在维度\(D\)中。这相当于使用大小和步长均为\(1\times 16 \times 16\)的卷积,将其显示为模型定义中的patch\(_1\)阶段。

接下来,对于长度为\(L\)、维度为\(D\)的投影序列的每个元素都加上一个位置嵌入\(\mathbf{E} \in \mathbb{R}^{L \times D}\),以编码位置信息并打破排列不变性。一个可学习的类别嵌入被添加到投影的图像补丁中。
将结果长度为\(L+1\)的序列依次输入到一个由\(N\)个transformer块构成的堆叠中进行处理,每个块都执行注意力(\(\operatorname{MHA}\))、多层感知机(\(\operatorname{MLP}\))和层归一化(\(\operatorname{LN}\))操作。假设\(X\)是块的输入,则单个transformer块的输出\(\operatorname{Block}(X)\)的计算方式为:
\[ X_1 = \operatorname{MHA}(\operatorname{LN}(X)) + X \\ \operatorname{Block}(X) = \operatorname{MLP}(\operatorname{LN}(X_1)) + X_1 \]
经过 \(N\) 个连续的块处理后,得到的序列进行层归一化,然后提取类嵌入并通过线性层传递以预测所需的输出(例如类别)。默认情况下,MLP 的隐藏维度为 \(4D\)。
MViT
MViT的关键是在整个网络中同时逐步“增加”通道分辨率(即维度)并“降低”时空分辨率(即序列长度)。MViT架构在早期层中具有细节的时空(和“粗略”的通道)分辨率,这些分辨率在后期层中进行上/下采样以获得粗略的时空(和“精细”的通道)分辨率。

一个scale stage被定义为在相同scale上操作的一组\(N\)个transformer块,其在通道和时空维度上具有相同的分辨率\(D\times T\times H\times W\)。在输入(cube\(_1\))中,将图像块(或立方体)投影到较小的通道维度(例如,比典型的ViT模型小8倍),但有更长的序列(例如,比典型的ViT模型密集16倍)。
在一个阶段的“过渡”(例如从scale\(_1\)到scale\(_2\)),被处理的序列的通道维度被上采样,而序列的长度则被下采样。这有效地降低了底层视觉数据的时空分辨率,同时允许网络在更复杂的特征中同化处理的信息。
通道扩展:通过将前一个阶段的最终MLP层的输出增加一个相对于引入的分辨率变化因子来扩展通道维度。具体来说,如果我们将时空分辨率下采样4倍,则将通道维度增加2倍。例如,从scale\(_3\)到scale\(_4\)的分辨率从\(2D\times \frac{T}{s_T}\times \frac{H}{8}\times \frac{T}{8}\)变为\(4D\times \frac{T}{s_T}\times \frac{H}{16}\times \frac{T}{16}\),类似于卷积。
Query 池化:池化注意力操作不仅可以灵活地调整Key和value的长度,还可以调整query及输出序列的长度。将查询向量\(\mathcal{P}(Q; \mathbf{k}; \mathbf{p}; \mathbf{s})\)与核\(\mathbf{s} \equiv (s^Q_T,s^Q_H,s^Q_W)\)进行池化操作,可以将序列的长度缩小\(s^Q_T \cdot s^Q_H \cdot s^Q_W\)倍。由于是在每个阶段开始时减小分辨率,然后在整个阶段中保持这种分辨率,因此每个阶段只有第一个池化注意力操作为\(\mathbf{s}^Q > 1\),而所有其他的\(\mathbf{s}^Q\)均为1
Key-Value 池化:与查询池化不同,更改\(K\) 和 \(V\) 的序列长度不会改变输出序列长度,因此也不会改变空时分辨率。作者将\(K,V\)和\(Q\)池化的使用解耦,\(Q\)池化用于每个阶段的第一层,而\(K,V\)池化则在所有其他层中使用。由于需要保证键和值张量的序列长度相同才能进行注意力权重计算,所以用于\(K\)和\(V\)张量的池化步长需要相同。在默认设置中,所有池化参数(\(\mathbf{k}; \mathbf{p}; \mathbf{s}\))限制是相同的,即\(\Theta_K \equiv \Theta_V\)在每个阶段内,但是根据不同阶段的尺度,自适应地变化\(\mathbf{s}\)。
跳过连接:由于维度问题,需要对查询池化算子 \(\mathcal{P}(\cdot ; \mathbf{\Theta}_Q)\) 来处理残差连接,需要将池化后的输入 \(X\) 加入到输出中,而不是直接将输入 \(X\) 加入到输出中,从而使分辨率匹配注意力查询 \(Q\)。
为了处理阶段之间通道维度的不匹配,作者使用了一个额外的线性层,对MHPA操作的层归一化输出进行操作。请注意,这与其他(保留分辨率)的跳跃连接不同,它们在未标准化的信号上进行操作。
