XVit

Posted on 2023-03-17 Edited on 2024-03-06 In 视频动作识别

摘要

本文研究的是利用Transformer进行视频识别。最近在这一领域的尝试在识别精度方面已经证明了有希望的结果，但在许多情况下，由于对时间信息的额外建模，它们也被证明会导致显著的计算开销。在这项工作中，我们提出了一个视频Transformer模型，其复杂性与视频序列中的帧数成线性比例，因此与基于图像的Transformer模型相比没有开销。为了实现这一点，我们的模型对视频Transformer中使用的全时空注意力做了两个近似:(a)它将时间注意力限制在局部时间窗口，并利用Transformer的深度来获得视频序列的全时间覆盖。(b)它使用高效的时空混合来联合关注空间和时间位置，而不会在纯空间注意力模型的基础上产生任何额外的成本。我们还展示了如何集成2个非常轻量级的全局时间关注机制，以最小的计算成本提供额外的精度改进。我们证明了我们的模型在最流行的视频识别数据集上产生非常高的识别精度，同时比其他视频转换器模型更有效。代码将被提供。

Different approaches to space-time self-attention for video recognition.

主要贡献

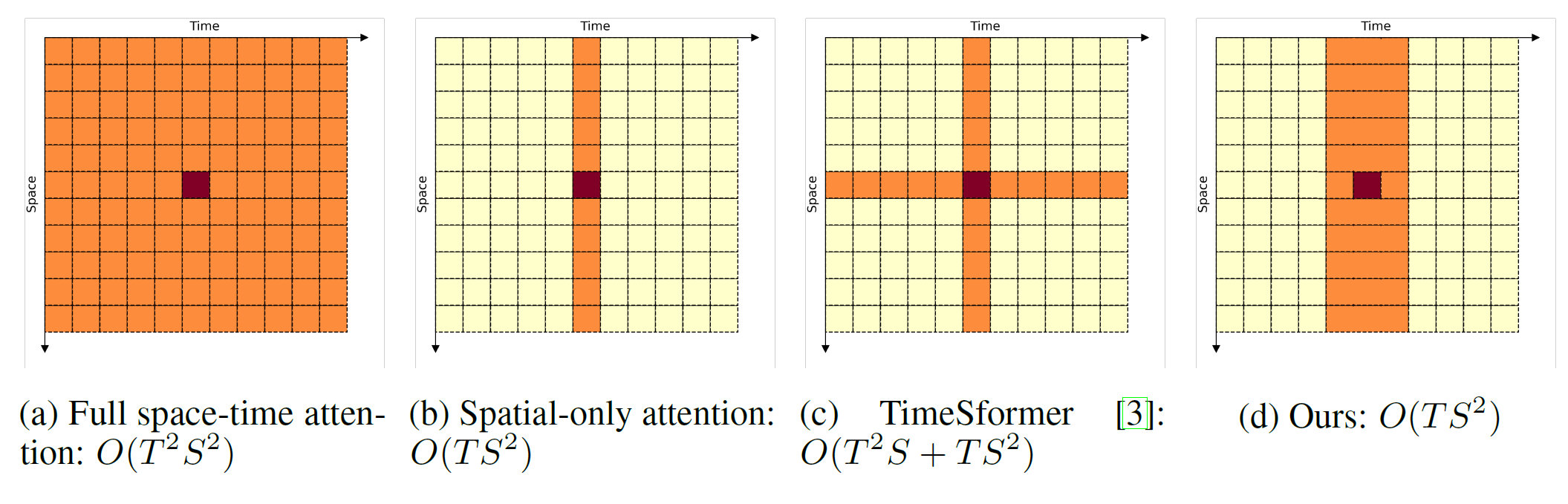
提出一种复杂度为$O(TS^2)$的视频Transformer模型，与基线模型一样高效。它在效率方面（即准确度/FLOP）比最近/同时提出的工作优越很多；
对视频Transformer的全时空注意力进行了两次近似：
1. 将时间注意力限制在局部时间窗口内，并利用Transformer的深度获得视频序列的完整时间覆盖；
2. 使用高效的时空混合，在不增加空间唯一注意力模型额外成本的情况下，共同关注空间和时间位置；
展示了如何整合两种非常轻量级的全局时间唯一注意力机制，它们以最小的计算成本提供额外的准确性改进。

方法

Video Transformer

给定视频片段：$\mathbf{X}\in\mathbb{R}^{T\times H \times W \times C }$

根据ViT，每帧将被分割为$K\times K$个非重叠补丁并通过一个线性embedding层$\mathbf{E}\in\mathbb{R}^{3K^2 \times d}$映射为visual token。另外需要学习两个位置embedding加载初始化的visual token，一是$\mathbf{p}_{s}\in\mathbb{R}^{1 \times S\times d}$，二是$\mathbf{p}_{t}\in\mathbb{R}^{T\times 1 \times d}$。最后token序列会被L层Transformer处理。第$l$层的visual token被定义为： \[ \mathbf{z}^l_{s,t}\in\mathbb{R}^d, \;\;\; l=0,\dots,L-1, \;\; s=0,\dots,S-1, \;\; t=0,\dots,T-1 \] 同样，cls token $\mathbf{z}^l_{cls}\in\mathbb{R}^{d}$会被加在token序列。第$l$层变换器使用一系列多头自我注意力（MSA）、层归一化（LN）和MLP（$\mathbb{R}^d \rightarrow \mathbb{R}^{4d} \rightarrow \mathbb{R}^d$）层来处理前一层的视觉标记$\mathbf{Z}^l\in\mathbb{R}^{(TS+1) \times d}$，如下所示： \[ \mathbf{Y}^{l} = \textrm{MSA}(\textrm{LN}(\mathbf{Z}^{l-1})) + \mathbf{Z}^{l-1},\\ \mathbf{Z}^{l+1} = \textrm{MLP}(\textrm{LN}(\mathbf{Y}^{l})) + \mathbf{Y}^{l}. \] 单个时空注意力的计算可被表示为 \[ \mathbf{y}^{l}_{s,t} = \sum_{t'=0}^{T-1} \sum_{s'=0}^{S-1} \textrm{Softmax}\{(\mathbf{q}^{l}_{s,t} \cdot \mathbf{k}^{l}_{s',t'})/\sqrt{d_h}\} \mathbf{v}^{l}_{s',t'}, \; \] 最后，整个模型的复杂度为: $O(3hTSdd_h)$ ($qkv$ projections) $+ O(2hT^2S^2d_h)$ (MSA for $h$ attention heads) $+ O(TS(hd_h)d)$ (multi-head projection) $+ O(4TSd^2)$ (MLP).

近似全时空注意力

Baseline是一个通过在每个Transformer层应用纯空间注意力来执行对全时空注意力的简单近似的模型: $$ ^{{l}{s,t} = {s'=0}}{S-1} {(^{l}{s,t} ^{l}{s',t})/} ^{l}_{s',t}, ;{ \[\begin{smallmatrix} s=0,\dots,S-1\\ t=0,\dots,T-1 \end{smallmatrix}\]

}

$$ 复杂度为$O(TS^2)$。在仅spatial-only注意力之后，对cls-token执行简单的时间平均 $\mathbf{z}_{final} = \frac{1}{T}\sum\limits_{t} \mathbf{z}^{L-1}_{t,cls}$以获得一个特征，该特征被馈送到线性分类器。

而TimeSFormer提出的factorised attention如下： $$ \[\begin{split} \tilde{\mathbf{y} }^{l}_{s,t} = \sum_{t'=0}^{T-1} \textrm{Softmax}\{(\mathbf{q}^{l}_{s,t} \cdot \mathbf{k}^{l}_{s,t'})/\sqrt{d_h}\} \mathbf{v}^{l}_{s,t'}, \\ \mathbf{y}^{l}_{s,t} = \sum_{s'=0}^{S-1} \textrm{Softmax}\{\tilde{\mathbf{q} }^{l}_{s,t} \cdot \tilde{\mathbf{k} }^{l}_{s',t})/\sqrt{d_h}\} \tilde{\mathbf{v} }^{l}_{s',t}, \end{split} \quad \begin{split} \; \begin{Bmatrix} s=0,\dots,S-1\\ t=0,\dots,T-1 \end{Bmatrix}, \end{split}\]

$$ 并且把复杂度降低到$O(T^2S + TS^2)$。然而，时间注意是对固定的空间位置进行的，当有相机或物体运动以及帧间存在空间错位时，时间注意是无效的。

模型旨在更好地近似完整的时空自注意力（SA），同时将复杂度保持在$O(TS^2)$，即不对spatial-only模型产生进一步的复杂性。为了达到这个目的，论文提出了第一次近似，以执行全时空注意力，但仅限于局部时间窗口$[-t_w, t_w]$： \[ \mathbf{y}^{l}_{s,t} = \sum_{t'=t-t_w}^{t+t_w} \sum_{s'=0}^{S-1} \textrm{Softmax}\{(\mathbf{q}^{l}_{s,t} \cdot \mathbf{k}^{l}_{s',t'})/\sqrt{d_h}\} \mathbf{v}^{l}_{s',t'}= \sum_{t'=t-t_w}^{t+t_w} \mathbf{V}^{l}_{t'} \mathbf{a}^l_{t'}, \;\big\{\begin{smallmatrix} s=0,\dots,S-1\\ t=0,\dots,T-1 \end{smallmatrix}\big\} \] 其中$\mathbf{V}^{l}_{t'}=[\mathbf{v}^{l}_{0,t'}; \mathbf{v}^{l}_{1,t'}; \dots; \mathbf{v}^{l}_{S-1,t'}]\in\mathbb{R}^{d_h \times S}$，$\mathbf{a}^l_{t'}=[a^l_{0,t'}, a^l_{1,t'}, \dots, a^l_{S-1,t'}]\in\mathbb{R}^{S}$是向量与相应的注意权重。对于单个 Transformer 层，$\mathbf{y}^{l}_{s,t}$ 是局部窗口 $[-t_w, t_w]$ 中视觉标记的时空组合。因此，在 $k$ 个 Transformer 层之后，$\mathbf{y}^{l+k}_{s,t}$ 将是局部窗口 $[-kt_w, kt_w]$ 中视觉标记的时空组合，这反过来方便地允许对整个剪辑执行时空注意力。例如，对于 $t_w=1$ 和 $k=4$，局部窗口变为 $[-4, 4]$，它在典型情况下覆盖整个视频剪辑（$T=8$）。

如上的局部自注意力的复杂度为 $O((2t_w+1)TS^2)$。为了进一步降低这个复杂度，在第一次近似之上进行第二次近似，如下所示：在空间位置 $s$ 和 $s’$ 之间的注意力是 \[ \sum_{t'=t-t_w}^{t+t_w} \textrm{Softmax}\{(\mathbf{q}^{l}_{s,t} \cdot \mathbf{k}^{l}_{s',t'})/\sqrt{d_h}\} \mathbf{v}^{l}_{s',t'} \] 即它需要计算 $2t_w+1$ 个注意力，每个时间位置在 $[-t_w, t_w]$ 上计算一个。相反，论文建议在 $[-t_w, t_w]$ 上计算一个注意力，这可以通过 $\mathbf{q}^{l}_{s,t}$ 关注 $\mathbf{k}^{l}_{s’,-t_w:t_w} \triangleq [\mathbf{k}{l}_{s’,t-t_w};\dots;\mathbf{k}{l}_{s’,t+t_w}] \in \mathbb{R}^{(2t_w+1)d_h}$ 来实现。注意，为了匹配 $\mathbf{q}^{l}_{s,t}$ 和 $\mathbf{k}^{l}_{s’,-t_w:t_w}$ 的维度，通常需要对 $\mathbf{k}^{l}_{s’,-t_w:t_w}$ 进行进一步投影到 $\mathbb{R}^{d_h}$，其复杂度为 $O((2t_w+1)d_h^2)$。为了缓解这种情况，使用移位技巧（类似TSM），它允许在 $O(d_h)$ 内同时执行零成本降维、时空混合和注意力（在 $\mathbf{q}^{l}_{s,t}$ 和 $\mathbf{k}^{l}_{s’,-t_w:t_w}$ 之间）。具体来说，每个 $t’ \in [-t_w, t_w]$ 被分配 $d_h^{t’}$ 个来自 $d_h$ 的通道（即 $\sum_{t’} d_h^{t’} = d_h$）。设 $\mathbf{k}^{l}_{s’,t’}(d_h^{t’})\in \mathbb{R}^{d_h^{t’} }$ 表示索引 $\mathbf{k}^{l}_{s’,t’}$ 中的 $d_h^{t’}$ 个通道的运算符。然后，构造一个新的key向量：

\[ \tilde{\mathbf{k} }^{l}_{s',-t_w:t_w} \triangleq [\mathbf{k}^{l}_{s',t-t_w}(d_h^{t-t_w}), \dots, \mathbf{k}^{l}_{s',t+t_w}(d_h^{t+t_w})]\in \mathbb{R}^{d_h} \]

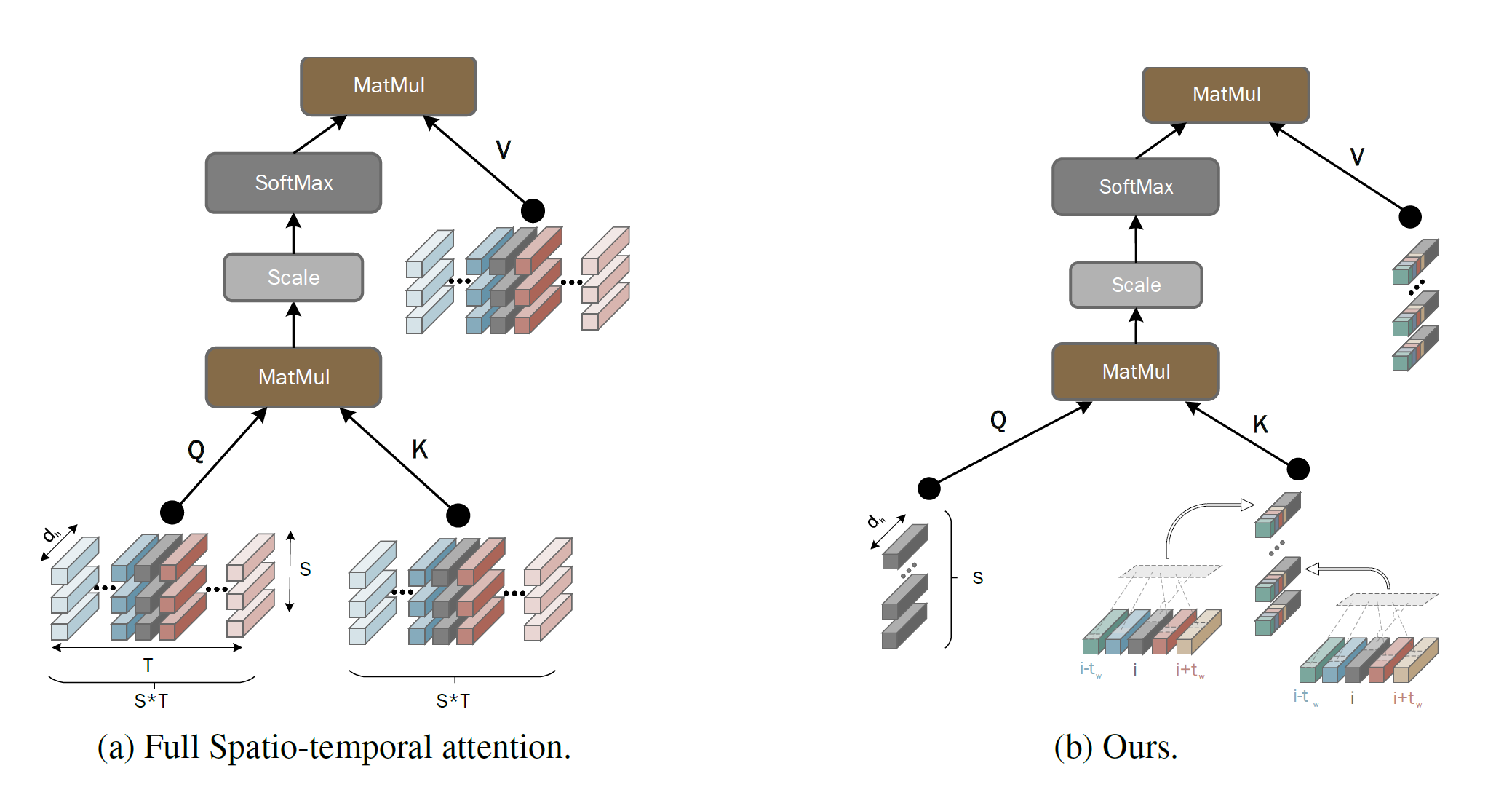
Detailed self-attention computation graph

上图展示了如何构造$\tilde{\mathbf{k} }^{l}_{s',-t_w:t_w}$，按照同样的方式可以构造一个新的value向量$\tilde{\mathbf{v} }^{l}_{s',-t_w:t_w}$。最后，提出的对全时空注意力的近似为:

\[ \mathbf{y}^{l_s}_{s,t} = \sum_{s'=0}^{S-1} \textrm{Softmax}\{(\mathbf{q}^{l_s}_{s,t} \cdot \tilde{\mathbf{k} }^{l}_{s',-t_w:t_w})/\sqrt{d_h}\} \tilde{\mathbf{v} }^{l}_{s',-t_w:t_w}, \;\big\{\begin{smallmatrix} s=0,\dots,S-1\\ t=0,\dots,T-1 \end{smallmatrix}\big\}. \]

Temporal Attention aggregation

最后一组cls-token$\mathbf{z}^{L-1}_{t,cls}, 0 \leq t \leq L-1$会被用于生成预测结果，为此，论文提出了两个方案：

在论文的baseline下，实验简单的时序平均$\mathbf{z}_{final} = \frac{1}{T}\sum_{t} \mathbf{z}^{L-1}_{t,cls}$
时间平均显然忽略了时序信息，因此论文提出使用轻量级的时间注意(TA)机制，该机制将参与$T$ 个cls-token。具体来说，token $\mathbf{z}_{final}$ 使用时序Transformer处理序列$[\mathbf{z}^{L-1}_{0,cls}, \ldots , \mathbf{z}^{L-1}_{T-1,cls}]$。这类似于ViViT的(并发)工作，不同之处在于，在模型中，发现一个单一的TA层就足够了，而ViViT使用$L_t$层。

Summary token

作为TA的替代方案，论文还提出了一种简单的轻量级机制，用于在网络中间层的不同帧之间进行信息交换。给定每一帧$t$的token集，$\mathbf{Z}_{t}^{l-1}\in\mathbb{R}^{(S+1)\times d_h}$（通过连接所有token$\mathbf{z}_{s,t}^{l-1}, s=0,\dots,S$来构造），计算得到$R$个token$\mathbf{Z}^{l}_{r, t} = \phi(\mathbf{Z}_{t}^{l-1})\in\mathbb{R}^{R\times d_h}$组成的一个新token集，这样的一个token集总结了帧信息，因此被命名为“摘要”token。然后将这些token附加到所有帧的visual token中，以计算key和value，以便query向量处理原始key和Summary标记。论文探讨了$\phi(.)$执行简单空间平均的情况，即$\mathbf{z}^{l}_{0, t} = \frac{1}{S}\sum_{s} \mathbf{z}^{l}_{s,t}$在每一帧的token上（对于这种情况，$R=1$）。请注意，对于$R=1$，Summary token引起的额外成本是$O(TS)$。

代码

模型整体

模型部分由ViT作为Base_model，在ViT的基础上主要修改了Attention部分，取其中一个Transformer_block打印如下所示：

(0): Block(
  (norm1): LayerNorm((768,), eps=1e-06, elementwise_affine=True)
  (attn): Attention(
    (qkv): Linear(in_features=768, out_features=2304, bias=True)
    (attn_drop): Dropout(p=0.0, inplace=False)
    (proj): Linear(in_features=768, out_features=768, bias=True)
    (proj_drop): Dropout(p=0, inplace=False)
    (control_point): AfterReconstruction()
    (control_point_query): TemporalShift(
      (net): AfterReconstruction()
    )
    (control_point_value): TemporalShift(
      (net): AfterReconstruction()
    )
  )
  (drop_path): Identity()
  (norm2): LayerNorm((768,), eps=1e-06, elementwise_affine=True)
  (mlp): Mlp(
    (fc1): Linear(in_features=768, out_features=3072, bias=True)
    (act): GELU(approximate='none')
    (fc2): Linear(in_features=3072, out_features=768, bias=True)
    (drop): Dropout(p=0, inplace=False)
  )
)

构建模型的代码主要位于video_model_builder.py，采用的是在base_model的基础上做修改的方式（基础模型应该是类似于TimesFormer中的联合时空的方式），make_temporal_shift应该就是论文提到的“移位技巧”的具体代码实现。

from timm.models import create_model
self.base_model = create_model()
if self.cfg.XVIT.USE_XVIT:
  make_temporal_shift(
      self.base_model,
      self.cfg.XVIT.NUM_SEGMENTS,
      n_div=self.cfg.XVIT.SHIFT_DIV,
      locations_list=self.cfg.XVIT.LOCATIONS_LIST,
  )

注意力

而注意力部分就是这篇论文的最主要的部分，相关代码在transformer_block.py，可以看到大多数的代码与ViT的一样，主要在Attention类做出了修改，对k和v做了构造，以达到对全时空注意力的近似：

1
2
3

if self.insert_control_point:
    k = self.control_point_query(k)
    v = self.control_point_value(v)

其中的control_point_query和control_point_value是一个继承nn.Identity类的名为AfterReconstruction的类，起到一个占位的作用，而在temporal_shift.py中的make_temporal_shift函数会用TemporalShift类去替代这个AfterReconstruction。

def make_temporal_shift(net, n_segment, n_div=8, locations_list=[]):
    n_segment_list = [n_segment] * 20
    assert n_segment_list[-1] > 0

    counter = 0
    for idx, block in enumerate(net.blocks):
        if idx in locations_list:
            net.blocks[idx].attn.control_point_query = TemporalShift(
                net.blocks[idx].attn.control_point_query,
                n_segment=n_segment_list[counter + 2],
                n_div=n_div,
            )
            net.blocks[idx].attn.control_point_value = TemporalShift(
                net.blocks[idx].attn.control_point_value,
                n_segment=n_segment_list[counter + 2],
                n_div=n_div,
            )
            counter += 1

class TemporalShift(nn.Module):
    def __init__(self, net, n_segment=3, n_div=8):
        super(TemporalShift, self).__init__()
        self.net = net
        self.n_segment = n_segment
        self.fold_div = n_div

    def forward(self, x):
        nt, num_heads, d, c = x.size()
        n_batch = nt // self.n_segment
        x = x.view(n_batch, self.n_segment, num_heads, d, c)
        fold = c * num_heads // self.fold_div

        x = (
            x.permute(0, 1, 2, 4, 3)
            .contiguous()
            .view(n_batch, self.n_segment, num_heads * c, d)
        )
        out = torch.zeros_like(x)
        out[:, :-1, :fold] = x[:, 1:, :fold]  # shift left
        out[:, 1:, fold : 2 * fold] = x[:, :-1, fold : 2 * fold]  # shift right
        out[:, :, 2 * fold :] = x[:, :, 2 * fold :]  # not shift

        out = (
            out.view(n_batch, self.n_segment, num_heads, c, d)
            .permute(0, 1, 2, 4, 3)
            .contiguous()
        )

        return out.view(nt, num_heads, d, c)

可以看到TemporalShift部分代码就是TSM的代码temporal-shift-module，也就是说XViT类似于ViT以TSM的方式去获得时序信息。

Temporal Attention aggregation

论文采用轻量级的时间注意(TA)机制处理最后一层注意力层所输出的cls——token，相关代码在head_helper.py，如下所示

def forward(self, x, position_ids):
    # temporal encoder (Longformer)
    B, D, E = x.shape

    cls_tokens = self.cls_token.expand(
        B, -1, -1
    )  # stole cls_tokens impl from Phil Wang, thanks
    x = torch.cat((cls_tokens, x), dim=1)
    x = self.temporal_encoder(x)
    # MLP head
    x = self.mlp_head(x[:, 0])
    return x

From ChatGPT (Just for fun)

Summary: The paper proposes a video recognition model using Transformers that scales linearly with the number of frames and avoids computational overhead by approximating space-time attention with local temporal windows and efficient space-time mixing.

Core Problems and Solutions:

Computational overhead induced by modeling temporal information in video recognition with Transformers. (Solution: proposing a model that scales linearly with the number of frames by approximating space-time attention with local temporal windows and efficient space-time mixing).

Main Insights and Lessons Learned:

The proposed video recognition model achieves state-of-the-art results while avoiding computational overheads.
The use of local temporal windows and efficient space-time mixing can significantly reduce the complexity of video recognition models.

Questions:

How does the proposed video recognition model compare to existing models in terms of recognition accuracy?
How does the model's efficiency compare to other approaches that avoid computational overhead in video recognition?
Can the proposed approach be extended to other applications that use video data, such as action recognition or video captioning?

Future Research Directions:

Investigating the impact of the proposed model on different video recognition tasks and datasets.
Exploring the use of local temporal windows and efficient space-time mixing in other areas of video analysis, such as action recognition or video captioning.
Extending the proposed approach to incorporate other types of attention mechanisms or to combine it with other efficient architectures for video recognition.

Relevant Documents:

"Attention is All You Need" by Vaswani et al.
"Temporal Segment Networks: Towards Good Practices for Deep Action Recognition" by Wang et al.
"Deep Residual Learning for Image Recognition" by He et al.
"A Closer Look at Spatiotemporal Convolutions for Action Recognition" by Tran et al.
"Convolutional Sequence to Sequence Learning" by Gehring et al.✏