TimeSFormer与ViViT

Posted on Edited on In

TimeSFormer

paper code

摘要

我们提出了一种基于空间和时间上的自注意力机制的无卷积视频分类方法。我们的方法，命名为“TimeSformer”，通过从一系列帧级别的图像块直接进行时空特征学习，将标准的Transformer架构适应到视频上。我们的实验研究比较了不同的自注意力方案，并发现“分割注意力”架构，在每个网络块中分别应用时间注意力和空间注意力，能够在我们考虑的设计选择中获得最佳的视频分类准确率。尽管设计完全不同，TimeSformer在几个动作识别基准上都达到了最先进的结果，包括在Kinetics-400和Kinetics-600上获得了最佳的准确率。最后，与3D卷积网络相比，我们的模型训练速度更快，可以实现更高的测试效率（以较小的准确率损失为代价），并且可以应用于更长的视频片段（超过一分钟）。

整体架构

输入视频：TimeSformer的输入为\(X \in \mathbb{R}^{H \times W \times 3 \times F}\)，表示\(F\)个size为\(H\times W\)的RGB帧。

转换为Patch：与ViT一样，将每一帧分解为N个不重叠的Patch，每一个patch的大小都为\(P \times P\)，因此\(N = HW/P^2\)。把patch展开为向量\(\mathbf{x}_{(p, t)} \in \mathbb{R}^{3 P^{2}}\)，其中\(p = 1, \dots , N\)表示空间位置，\(t = 1, \dots ,F\)为时间帧的索引。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class PatchEmbed(nn.Module):
    """ Image to Patch Embedding
    """
    def __init__(self, img_size=224, patch_size=16, in_chans=3, embed_dim=768):
        super().__init__()
        img_size = to_2tuple(img_size)
        patch_size = to_2tuple(patch_size)
        num_patches = (img_size[1] // patch_size[1]) * (img_size[0] // patch_size[0])
        self.img_size = img_size
        self.patch_size = patch_size
        self.num_patches = num_patches

        self.proj = nn.Conv2d(in_chans, embed_dim, kernel_size=patch_size, stride=patch_size)

        def forward(self, x):
            B, C, T, H, W = x.shape
            x = rearrange(x, 'b c t h w -> (b t) c h w')
            x = self.proj(x) # ((bt), dim, h//p, w//p)
            W = x.size(-1)
            x = x.flatten(2).transpose(1, 2)# ((bt), (hw)//(p^2), dim)
            return x, T, W

Linear embedding：将\(\mathbf{x}_{(p, t)} \in \mathbb{R}^{3 P^{2}}\)线性映射到\(\mathbf{z}_{(p, t)}^{(0)} \in \mathbb{R}^{D}\)： \[ \mathbf{z}_{(p, t)}^{(0)}=E \mathbf{x}_{(p, t)}+\mathbf{e}_{(p, t)}^{p o s} \] 其中，\(E \in \mathbb{R}^{D \times 3 P^{2}}\)为可学习的线性映射系数矩阵，\(\mathbf{e}^{pos}_{(p,t)} \in \mathbb{R} ^ D\)为可学习的空间位置编码，\(\mathbf{z}_{(p, t)}\) 序列是Transformer的输入。与ViT一样，在序列的第一个位置加入一个可学习的向量\(\mathbf{z}_{(0, 0)}\)作为cls-token。

1
2
3
4
5
B = x.shape[0]
x, T, W = self.patch_embed(x)
cls_tokens = self.cls_token.expand(x.size(0), -1, -1)
x = torch.cat((cls_tokens, x), dim=1)
x = x + self.pos_embed # pose embeding

QKV计算：Transformer包含\(L\)层encoding blocks，每个block的query、key、value表达为 \[ \begin{array}{l} \mathbf{q}_{(p, t)}^{(\ell, a)}=W_{Q}^{(\ell, a)} \operatorname{LN}\left(\mathbf{z}_{(p, t)}^{(\ell-1)}\right) \in \mathbb{R}^{D_{h}} \\ \mathbf{k}_{(p, t)}^{(\ell, a)}=W_{K}^{(\ell, a)} \operatorname{LN}\left(\mathbf{z}_{(p, t)}^{(\ell-1)}\right) \in \mathbb{R}^{D_{h}} \\ \mathbf{v}_{(p, t)}^{(\ell, a)}=W_{V}^{(\ell, a)} \operatorname{LN}\left(\mathbf{z}_{(p, t)}^{(\ell-1)}\right) \in \mathbb{R}^{D_{h}} \end{array} \] 其中，\(a = 1 , \dots,A\)代表注意力头的数量，\(D_h\)代表每个head的维度

自注意力计算：对于自注意力计算部分，论文给出了五种不同的方式，将在下一节详细介绍。对于query patch\((p,t)\)的自注意力权重\(\boldsymbol{\alpha}_{(p, t)}^{(\ell, a)} \in \mathbb{R}^{N F+1}\)通用的给出如下： \[ \boldsymbol{\alpha}_{(p, t)}^{(\ell, a)}=\operatorname{SM}\left(\frac{\mathbf{q}_{(p, t)}^{(\ell, a)}}{\sqrt{D_{h}}} \cdot\left[\mathbf{k}_{(0,0)}^{(\ell, a)}\left\{\mathbf{k}_{\left(p^{\prime}, t^{\prime}\right)}^{(\ell, a)}\right\}_{\substack{p^{\prime}=1, \ldots, N \\ t^{\prime}=1, \ldots, F}}\right]\right) \] 编码：第\(\ell\)个编码\(\mathbf{z}_{(p, t)}^{(\ell)}\)是利用每个注意头的自注意系数计算值向量的加权和得到： \[ \mathbf{s}_{(p, t)}^{(\ell, a)}=\alpha_{(p, t),(0,0)}^{(\ell, a)} \mathbf{v}_{(0,0)}^{(\ell, a)}+\sum_{p^{\prime}=1}^{N} \sum_{t^{\prime}=1}^{F} \alpha_{(p, t),\left(p^{\prime}, t^{\prime}\right)}^{(\ell, a)} \mathbf{v}_{\left(p^{\prime}, t^{\prime}\right)}^{(\ell, a)} \] 然后，将来自所有head的这些向量的拼接映射并通过MLP，这两个操作都具有残差连接： \[ \begin{array}{l} \mathbf{z}_{(p, t)}^{\prime(\ell)}=W_{O}\left[\begin{array}{c} \mathbf{s}_{(p, t)}^{(\ell, 1)} \\ \vdots \\ \mathbf{s}_{(p, t)}^{(\ell, \mathcal{A})} \end{array}\right]+\mathbf{z}_{(p, t)}^{(\ell-1)} \\ \mathbf{z}_{(p, t)}^{(\ell)}=\operatorname{MLP}\left(\operatorname{LN}\left(\mathbf{z}_{(p, t)}^{\prime(\ell)}\right)\right)+\mathbf{z}_{(p, t)}^{\prime(\ell)} . \end{array} \] 分类 embedding 取出cls-token用作最终的分类： \[ y = MLP(LN(\mathbf{z}^{(L)}_{(0, 0)})) \]

自注意力机制

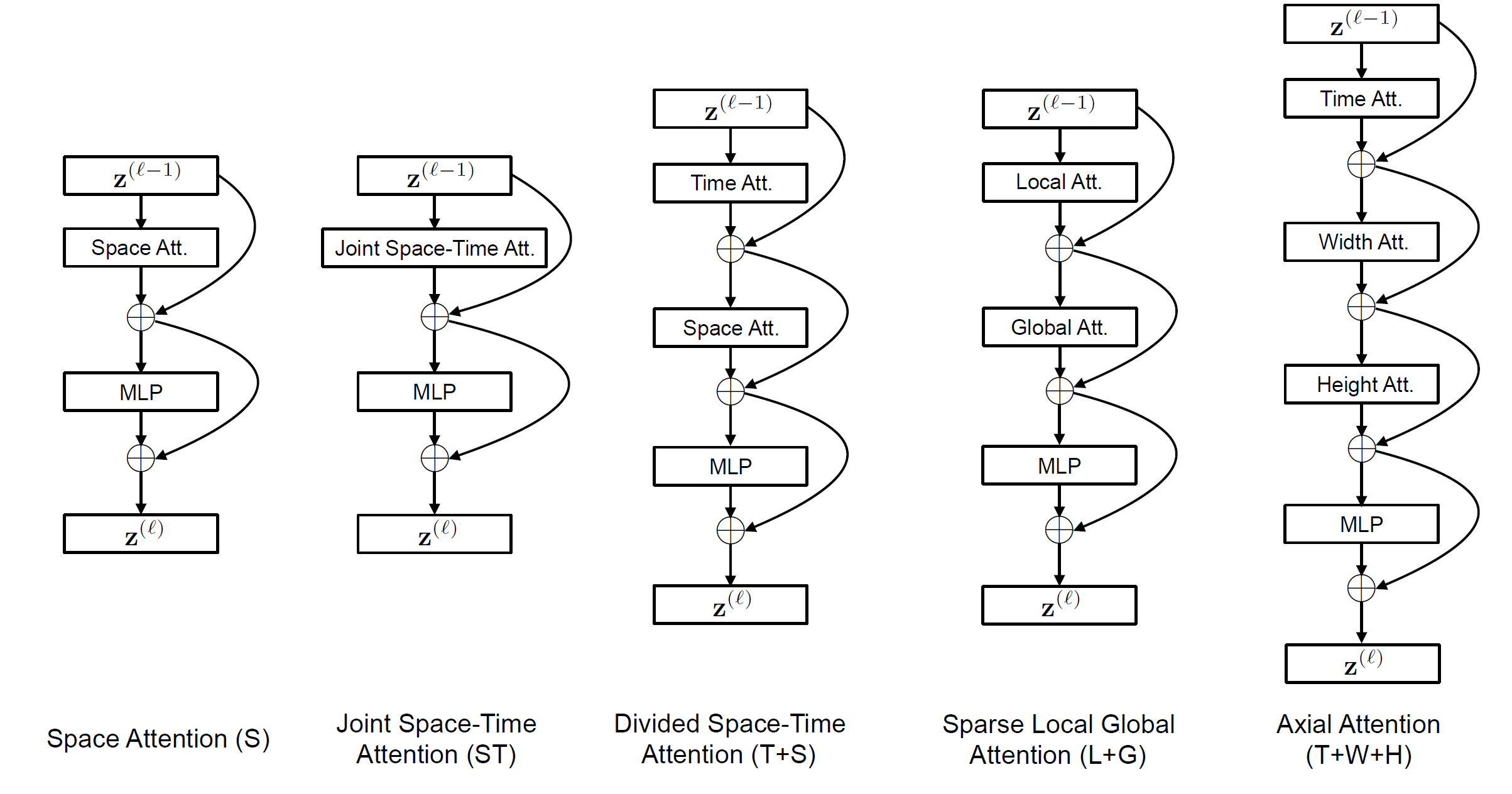
论文研究的视频自注意力块

通过对输入图像进行分块，论文中一共研究了五种不同的注意力机制：

  1. 空间注意力机制（S)：只取同一帧内的图像块进行自注意力机制
  2. 时空共同注意力机制（ST）：取所有帧中的所有图像块进行注意力机制
  3. 分开的时空注意力机制（T+S）：先对同一帧中的所有图像块进行自注意力机制，然后对不同帧中对应位置的图像块进行注意力机制
  4. 稀疏局部全局注意力机制（L+G）：先利用所有帧中，相邻的 H/2 和 W/2 的图像块计算局部的注意力，然后在空间上，使用2个图像块的步长，在整个序列中计算自注意力机制，这个可以看做全局的时空注意力更快的近似
  5. 轴向的注意力机制（T+W+H）：先在时间维度上进行自注意力机制，然后在纵坐标相同的图像块上进行自注意力机制，最后在横坐标相同的图像块上进行自注意力机制
论文研究的五种时空自注意力机制方案的可视化

Space Attention

Space Attention就是标准的Transformer结构，只计算空间注意力，跟ViT一样，只有\(N+1\)个query-key对。 \[ \boldsymbol{\alpha}_{(p, t)}^{(\ell, a) \text { space }}=\operatorname{SM}\left(\frac{\mathbf{q}_{(p, t)}^{(\ell, a)}}{\sqrt{D_{h}}} \cdot\left[\mathbf{k}_{(0,0)}^{(\ell, a)}\left\{\mathbf{k}_{\left(p^{\prime}, t\right)}^{(\ell, a)}\right\}_{p^{\prime}=1, \ldots, N}\right]\right) \] 代码部分，向量加上空间位置编码后，就可以输入到Attention blocks，而由于在转换patch的时候batchsize和t是并在一起的，所以需要转换回去，并多帧取平均。

1
2
3
4
5
6
7
8
## Attention blocks
for blk in self.blocks:
    x = blk(x, B, T, W)

### Predictions for space-only baseline
if self.attention_type == 'space_only':
    x = rearrange(x, '(b t) n m -> b t n m',b=B,t=T)
    x = torch.mean(x, 1) # averaging predictions for every frame

self.blocks如下：

1
2
3
4
5
6
7
num_spatial_tokens = (x.size(1) - 1) // T
H = num_spatial_tokens // W

if self.attention_type in ['space_only', 'joint_space_time']:
    x = x + self.drop_path(self.attn(self.norm1(x)))
    x = x + self.drop_path(self.mlp(self.norm2(x)))
    return x

Joint Space-Time Attention

\[ \boldsymbol{\alpha}_{(p, t)}^{(\ell, a)}=\operatorname{SM}\left(\frac{\mathbf{q}_{(p, t)}^{(\ell, a)}}{\sqrt{D_{h}}} \cdot\left[\mathbf{k}_{(0,0)}^{(\ell, a)}\left\{\mathbf{k}_{\left(p^{\prime}, t^{\prime}\right)}^{(\ell, a)}\right\}_{\substack{p^{\prime}=1, \ldots, N \\ t^{\prime}=1, \ldots, F}}\right]\right) \]

Joint Space-Time Attention需要在输入Transformer前先加上TimeEmbeeding，相关代码如下：

1
2
3
4
5
6
7
8
9
## Time Embeddings
if self.attention_type != 'space_only':
    cls_tokens = x[:B, 0, :].unsqueeze(1)
    x = x[:,1:]
    x = rearrange(x, '(b t) n m -> (b n) t m',b=B,t=T)
	x = x + self.time_embed
    x = self.time_drop(x)
    x = rearrange(x, '(b n) t m -> b (n t) m',b=B,t=T)
    x = torch.cat((cls_tokens, x), dim=1)

Divided Space-Time Attention

对于Divided Space-Time Attention，先计算时间自注意力如下： \[ \boldsymbol{\alpha}_{(p, t)}^{(\ell, a) \text { time }}=\operatorname{SM}\left(\frac{\mathbf{q}_{(p, t)}^{(\ell, a)^{\top}}}{\sqrt{D_{h}}} \cdot\left[\mathbf{k}_{(0,0)}^{(\ell, a)}\left\{\mathbf{k}_{\left(p, t^{\prime}\right)}^{(\ell, a)}\right\}_{t^{\prime}=1, \ldots, F}\right]\right) \] 得到时间注意力权重后，同样经过编码的操作，但不通过MLP，得到时间编码\(z'^{(\ell )time}_{(p,t)}\)。

通过时间编码可计算出响应的Q、K、V，计算空间自注意力如下： \[ \boldsymbol{\alpha}_{(p, t)}^{(\ell, a) \text { space }}=\operatorname{SM}\left(\frac{\mathbf{q}_{(p, t)}^{(\ell, a)}}{\sqrt{D_{h}}} \cdot\left[\mathbf{k}_{(0,0)}^{(\ell, a)}\left\{\mathbf{k}_{\left(p^{\prime}, t\right)}^{(\ell, a)}\right\}_{p^{\prime}=1, \ldots, N}\right]\right) \] 这样得到的自注意力权重就会包含时空信息。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
elif self.attention_type == 'divided_space_time':
    ## Temporal
    xt = x[:,1:,:]
    xt = rearrange(xt, 'b (h w t) m -> (b h w) t m',b=B,h=H,w=W,t=T)
    res_temporal = self.drop_path(self.temporal_attn(self.temporal_norm1(xt)))
    res_temporal = rearrange(res_temporal, '(b h w) t m -> b (h w t) m',b=B,h=H,w=W,t=T)
    res_temporal = self.temporal_fc(res_temporal)
    xt = x[:,1:,:] + res_temporal

    ## Spatial
    init_cls_token = x[:,0,:].unsqueeze(1)
    cls_token = init_cls_token.repeat(1, T, 1)
    cls_token = rearrange(cls_token, 'b t m -> (b t) m',b=B,t=T).unsqueeze(1)
    xs = xt
    xs = rearrange(xs, 'b (h w t) m -> (b t) (h w) m',b=B,h=H,w=W,t=T)
    xs = torch.cat((cls_token, xs), 1)
    res_spatial = self.drop_path(self.attn(self.norm1(xs)))

    ### Taking care of CLS token
    cls_token = res_spatial[:,0,:]
    cls_token = rearrange(cls_token, '(b t) m -> b t m',b=B,t=T)
    cls_token = torch.mean(cls_token,1,True) ## averaging for every frame
    res_spatial = res_spatial[:,1:,:]
    res_spatial = rearrange(res_spatial, '(b t) (h w) m -> b (h w t) m',b=B,h=H,w=W,t=T)
    res = res_spatial
    x = xt

    ## Mlp
    x = torch.cat((init_cls_token, x), 1) + torch.cat((cls_token, res), 1)
    x = x + self.drop_path(self.mlp(self.norm2(x)))
    return x

ViViT

paper code ## 摘要

这篇文章介绍了一种基于纯变换器的视频分类模型，该模型受到图像分类中此类模型的最近成功的启发。为了有效处理视频中可能遇到的大量时空token，我们提出了几种沿着空间和时间维度分解我们模型的方法，以提高效率和可扩展性。此外，为了在较小的数据集上有效地训练我们的模型，我们展示了如何在训练过程中对模型进行正则化并利用预训练的图像模型。我们进行了彻底的消融研究，并在多个视频分类基准测试中取得了最先进的结果，包括 Kinetics 400 和 600、Epic Kitchens、Something-Something v2 和 Moments in Time，优于基于深度 3D 卷积网络的先前方法。

ViT概述

视觉变换器 (ViT) 适应了变换器架构，以最小的改动来处理2D图像。 具体来说，ViT 提取 \(N\) 个不重叠的图像块，\(x_i \in \mathbb{R}^{h \times w}\)，执行线性投影，然后将它们栅格化为1Dtoken \(z_i \in \mathbb{R}^d\)。输入到下面的变换器编码器的token序列为 \[ \mathbf{z} = [z_{cls}, \mathbf{E}x_1, \mathbf{E}x_2, \ldots , \mathbf{E}x_N] + \mathbf{p} \] 其中，\(\mathbf{E}\) 的投影相当于2D卷积。一个可选的学习分类token \(z_{cls}\) 被添加到这个序列的前面，它在编码器的最后一层的表示作为分类层使用的最终表示。 此外，一个学习位置嵌入，\(\mathbf{p} \in \mathbb{R}^{N \times d}\)，被添加到token中以保留位置信息，因为变换器中后续的自注意力操作是排列不变的。 然后将token传递到由 \(L\) 个变换器层组成的编码器中。 每一层 \(\ell\) 都包括多头自注意力、层归一化 (LN) 和 MLP 块，如下所示： \[ \mathbf{y}^{\ell} = \text{MSA}(\text{LN}(\mathbf{z}^\ell)) +\mathbf{z}^\ell \\ \mathbf{z}^{\ell + 1} = \text{MLP}(\text{LN}(\mathbf{y}^\ell)) + \mathbf{y}^\ell \] MLP 由两个线性投影组成，它们之间由 GELU 非线性分隔，token维度 \(d\) 在所有层中保持不变。 最后，使用线性分类器根据 \(z_{cls}^L \in \mathbb{R}^d\) 对编码输入进行分类，如果它被添加到输入的前面，或者对所有token进行全局平均池化 \(\mathbf{z}^{L}\)。

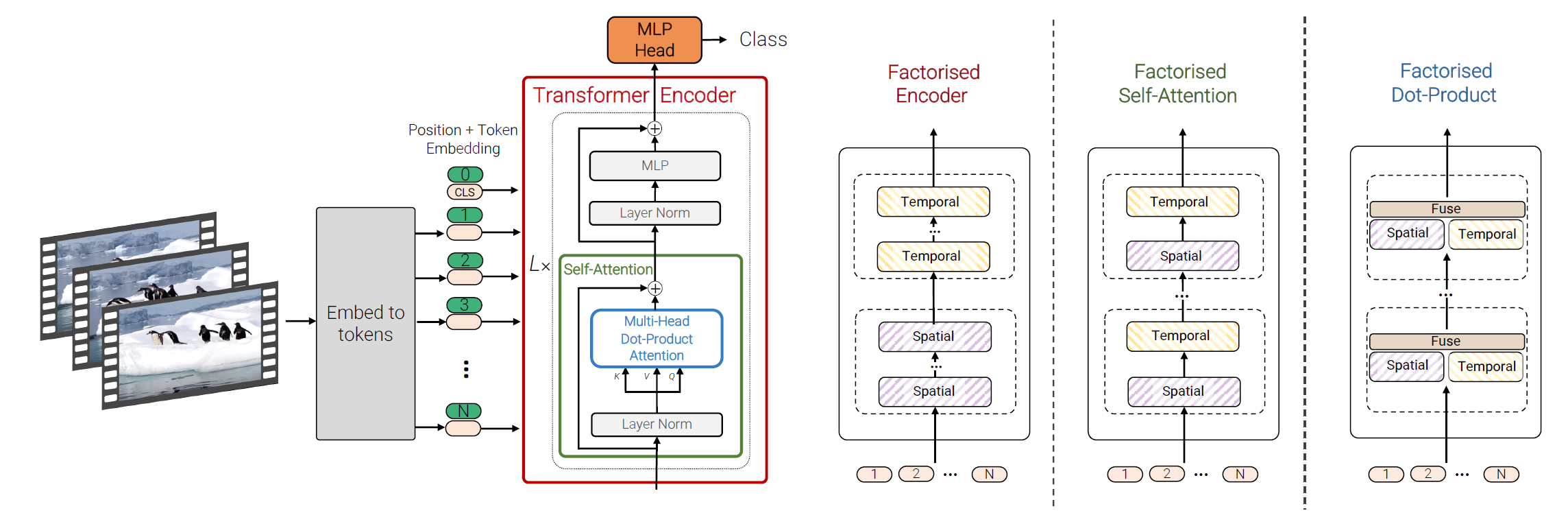
ViViT架构

视频片段 Embeeding

论文给出了两种方法把视频\(\mathbf{V} \in \mathbb{R}^{T \times H \times W \times C}\)映射到一个token序列\(\mathbf{\tilde{z}} \in \mathbb{R}^{n_t \times n_h \times n_w \times d}\)，接着加上位置embedding并reshape为\(\mathbb{R}^{N \times d}\)以得到transformer的输入\(\mathbf{z}\)。

Uniform frame sampling

Uniform frame sampling

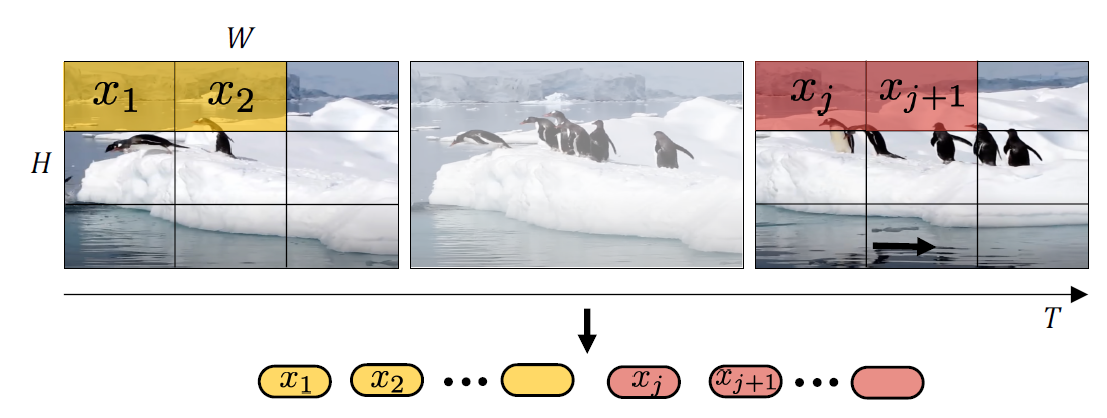
如图所示，标记输入视频的一种简单方法是从输入视频剪辑中均匀采样 \(n_t\) 帧，使用与 ViT 相同的方法独立嵌入每个 2D 帧，并将所有这些token连接在一起。 具体地，如果从每个帧中提取 \(n_h \cdot n_w\) 个不重叠的图像块，则总共有 \(n_t \cdot n_h \cdot n_w\) 个token将通过变换器编码器转发。 直观地，这个过程可以看作是简单地构造一个大的 2D 图像来按照 ViT 进行标记。 这种方法跟TimeSformer的一样。

Tubelet embedding

Tubelet embedding

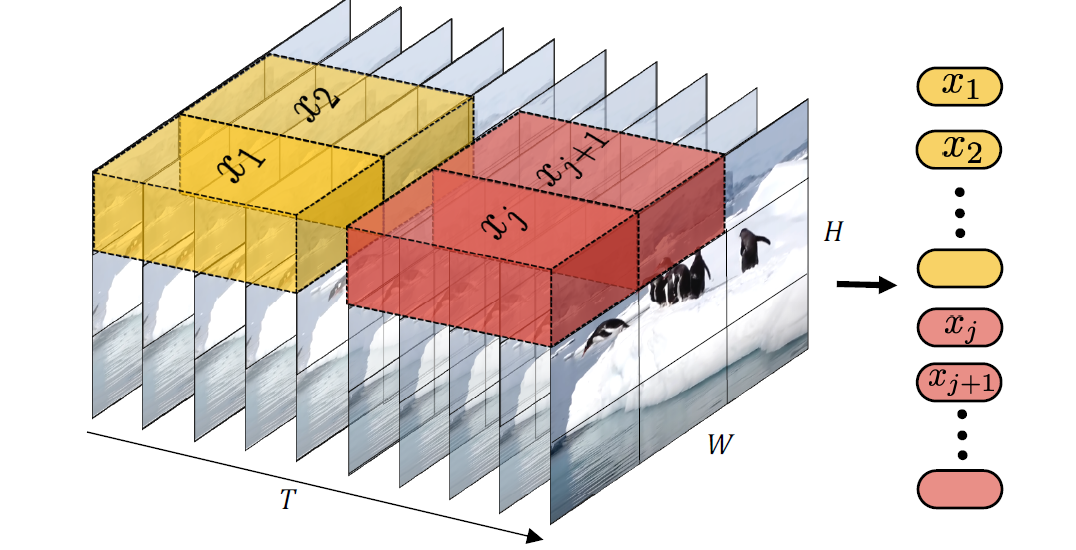
另一种方法，如图所示，是从输入体积中提取不重叠的时空“tubes”，并将其线性投影到 \(\mathbb{R}^d\)。 这种方法是 ViT embedding的 3D 扩展，类似于 3D 卷积。 对于一个维度为 \(t \times h \times w\) 的tubelet，\(n_t = \left\lfloor\frac{T}{t}\right\rfloor\)，\(n_h = \left\lfloor\frac{H}{h}\right\rfloor\) 和 \(n_w = \left\lfloor\frac{W}{w}\right\rfloor\)，分别从时间、高度和宽度维度提取token。 较小的tubelet尺寸因此会导致更多的token，增加了计算量。直观地说，这种方法在标记过程中融合了时空信息，而与“均匀帧采样”不同，在那里来自不同帧的时间信息由变换器融合。

视频Transformer 模型

Model 1: Spatio-temporal attention

这个模型跟TimeSformer中的Joint Space-Time Attention基本一致，简单地将所有的时空token\(\mathbf{z}^{0}\)输入到Transformer的编码器。而由于token的数量会随着采样帧的变多而变多，这样就会带来更大的计算复杂度。

Model 2: Factorised encoder

Model 2: Factorised encoder

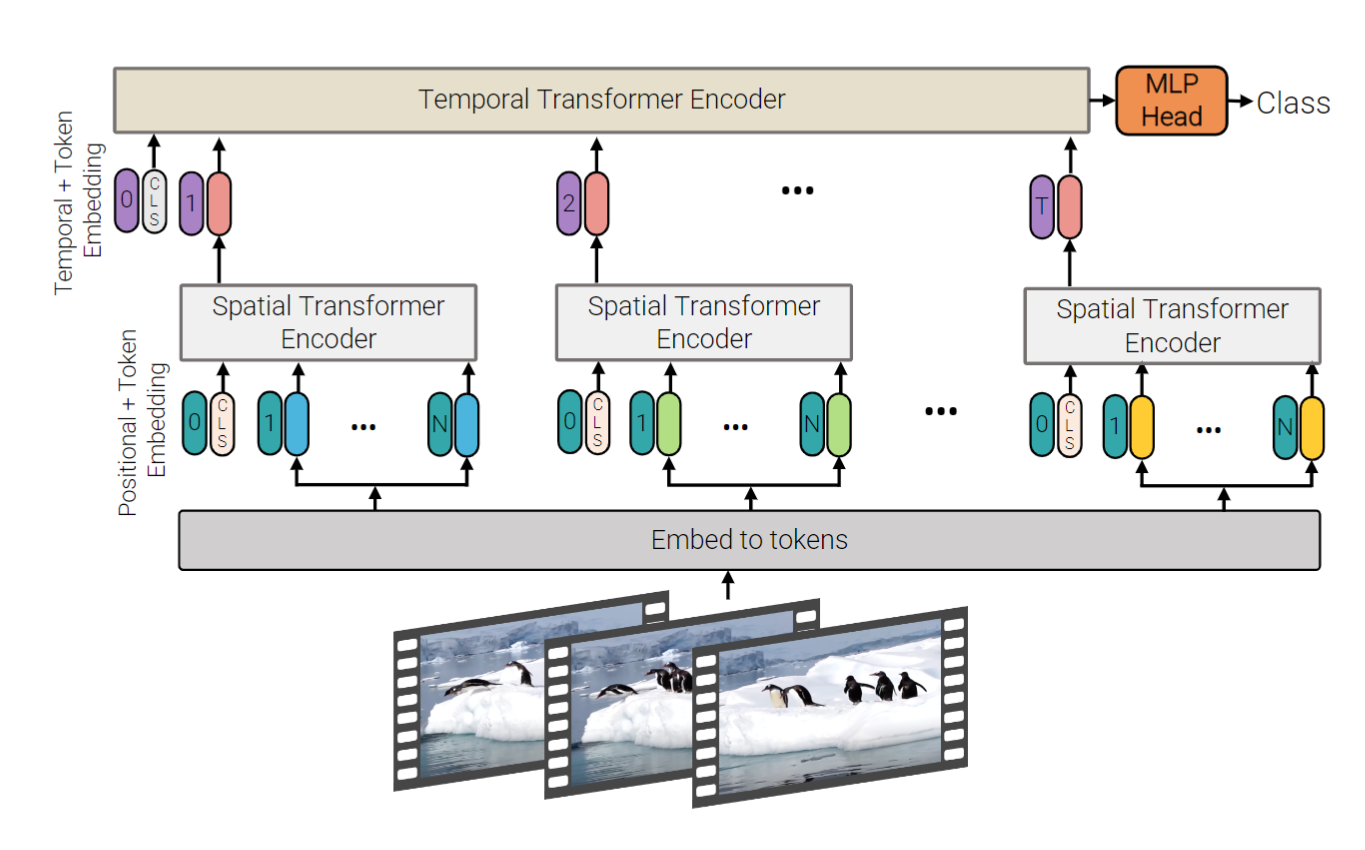
如图所示，该模型由两个独立的Transformer编码器组成。首先是空间编码器，仅以同一帧中提取的token为输入在\(L_s\)层后获得每帧的表示。\(z_{cls}^{L_s}\)是空间编码的cls-token，用于表达的空间特征。将每帧的特征cat以得到\(\mathbf{H} \in \mathbb{R}^{n_t \times d}\)输入到\(L_t\)个Transformer组成的时间编码器，以建模来自不同帧的token之间的特征交互，最后该编码器的cls-token用于分类。相比于模型1，计算复杂度从\(\mathcal{O}((n_t \cdot n_h \cdot n_w)^2)\)减低到\(\mathcal{O}({(n_h \cdot n_w)^2 + n_t^2)}\) 。

代码来自https://github.com/rishikksh20/ViViT-pytorch/blob/master/vivit.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def forward(self, x):
    x = self.to_patch_embedding(x)
    b, t, n, _ = x.shape
    cls_space_tokens = repeat(self.space_token, '() n d -> b t n d', b = b, t=t) # 按维度扩展
    x = torch.cat((cls_space_tokens, x), dim=2)
    x += self.pos_embedding[:, :, :(n + 1)]
    x = self.dropout(x)
    x = rearrange(x, 'b t n d -> (b t) n d')
    x = self.space_transformer(x)
    x = rearrange(x[:, 0], '(b t) ... -> b t ...', b=b) #提取每帧计算得到的cls-token
    cls_temporal_tokens = repeat(self.temporal_token, '() n d -> b n d', b=b)
    x = torch.cat((cls_temporal_tokens, x), dim=1)
    x = self.temporal_transformer(x)        
    x = x.mean(dim = 1) if self.pool == 'mean' else x[:, 0]
    return self.mlp_head(x)

Model 3: Factorised self-attention

Model 3: Factorised self-attention

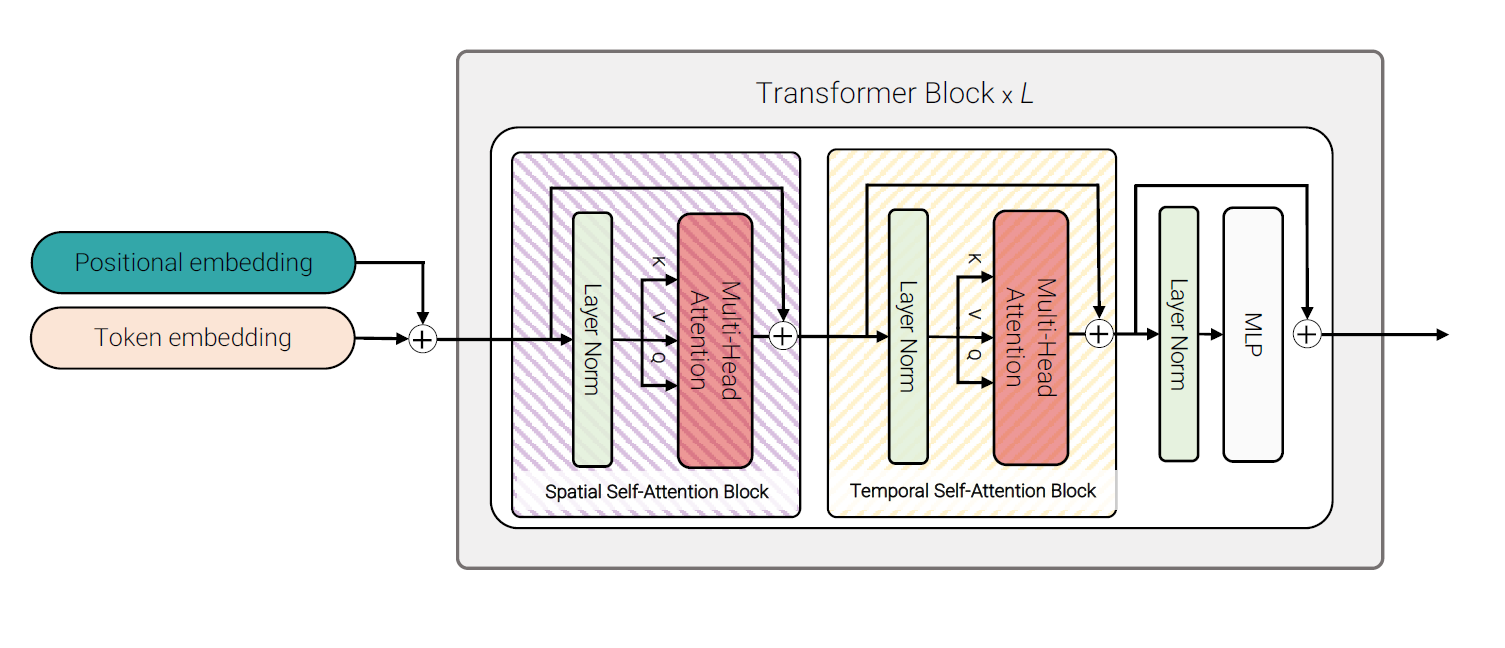
模型3与TimeSFormer的Divided Space-Time基本一致，不同的是没有使用cls-token，以避免在空间和时间维度之间重新构造输入token时产生歧义，而且他们的方法验证出无论是先空间自注意力还是时间自注意力结果是一样的。

Model 4: Factorised dot-product attention

Model 4: Factorised dot-product attention

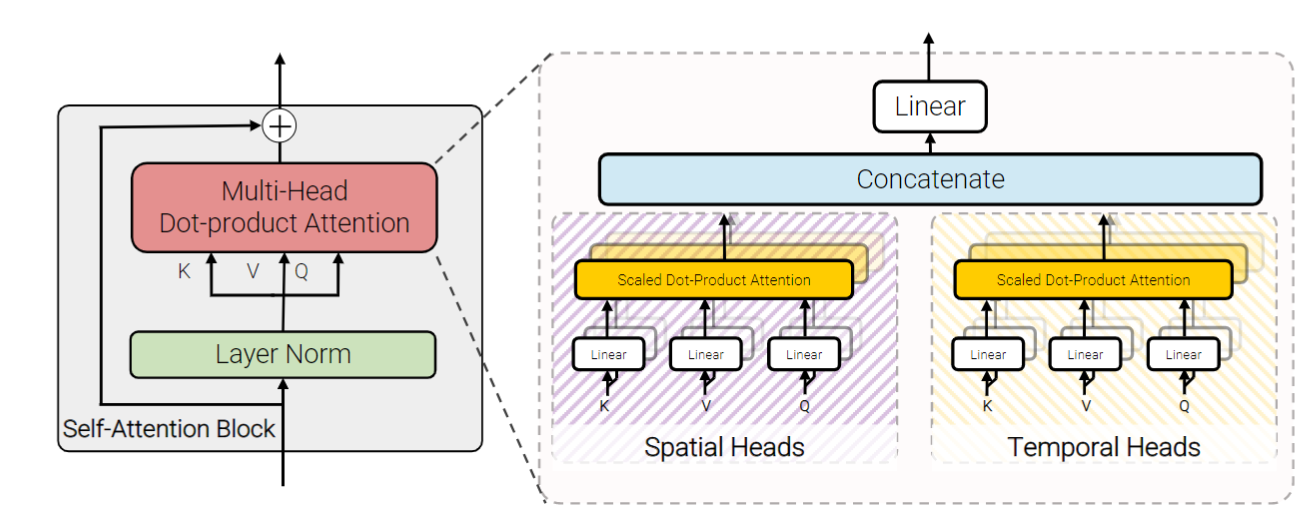
模型4一个与模型2和模型3具有相同计算复杂度的模型，同时保留了与未分解的模型1相同的参数数量。具体而言，模型4采用了不同的注意力头分别在空间和时间维度上计算每个token的注意权重，自注意操作被定义为 \[ Attention(\mathbf{Q}, \mathbf{K}, \mathbf{V}) = Softmax\left(\frac{\mathbf{Q} \mathbf{K}^\top}{\sqrt{d_k}} \right) \mathbf{V}. \label{eq:selfattn} \] 在自注意力中，查询\(\mathbf{Q} = \mathbf{X} \mathbf{W}_q\)，键\(\mathbf{K} = \mathbf{X} \mathbf{W}_k\)和值\(\mathbf{V}= \mathbf{X} \mathbf{W}_v\)是输入\(\mathbf{X}\)的线性投影，其中\(\mathbf{X}, \mathbf{Q}, \mathbf{K}, \mathbf{V} \in \mathbb{R}^{N \times d}\)。 注意，在未分解的情况下（模型1），空间和时间维度合并为\(N = n_t \cdot n_h \cdot n_w\)。

这里的主要思想是通过构造\(\mathbf{K}_s, \mathbf{V}_s \in \mathbb{R}^{n_h \cdot n_w \times d}\)和\(\mathbf{K}_t, \mathbf{V}_t \in \mathbb{R}^{n_t \times d}\)，即与这些维度对应的键和值，修改每个查询的键和值，以仅关注来自相同空间和时间索引的令牌。然后，对于一半的注意力头，通过计算\(\mathbf{Y}_s = Attention(\mathbf{Q}, \mathbf{K}_s, \mathbf{V}_s)\)来关注来自空间维度的token，对于其余部分，通过计算\(\mathbf{Y}_t = Attention(\mathbf{Q}, \mathbf{K}_t, \mathbf{V}_t)\)来关注时间维度。

鉴于只是为每个查询更改注意力邻域，注意力操作与未分解情况下具有相同的维度，即\(\mathbf{Y}_s, \mathbf{Y}_t \in\mathbb {R}^{N\times d}\)。 然后通过连接它们并使用线性投影来组合多个头的输出， $ =Concat（ _s, _t） _O $。

代码来自：https://github.com/noureldien/vivit_pytorch/blob/master/modules/vivit.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
def forward_space(self, x):
    """
    x: (b, t, n, d)
    """

    t = self.num_patches_time
    n = self.num_patches_space

    # hide time dimension into batch dimension
    x = rearrange(x, 'b t n d -> (b t) n d')  # (bt, n, d)

    # apply self-attention
    out = self.forward_attention(x)  # (bt, n, d)

    # recover time dimension and merge it into space
    out = rearrange(out, '(b t) n d -> b (t n) d', t=t, n=n)  # (b, tn, d)

    return out
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
def forward_time(self, x):
    """
    x: (b, t, n, d)
    """

    t = self.num_patches_time
    n = self.num_patches_space

    # hide time dimension into batch dimension
    x = x.permute(0, 2, 1, 3)  # (b, n, t, d)
    x = rearrange(x, 'b n t d -> (b n) t d')  # (bn, t, d)

    # apply self-attention
    out = self.forward_attention(x)  # (bn, t, d)

    # recover time dimension and merge it into space
    out = rearrange(out, '(b n) t d -> b (t n) d', t=t, n=n)  # (b, tn, d)

    return out
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def forward(self, x):

    t = self.num_patches_time
    n = self.num_patches_space

    # reshape to reveal dimensions of space and time
    x = rearrange(x, 'b (t n) d -> b t n d', t=t, n=n)

    if self.attn_type == 'space':
        out = self.forward_space(x) # (b, tn, d)
    elif self.attn_type == 'time':
        out = self.forward_time(x) # (b, tn, d)
    else:
        raise Exception('Unknown attention type: %s' % (self.attn_type))

    return out

利用预训练模型进行初始化

由于Transformer缺乏CNN那样的归纳偏置，因此往往需要大规模的数据集作为训练集。为了规避这个问题，类似于3D-CNN的方法用ImageNet上预训练的2D-CNN网络（如Resnet等），使用了在大规模图片数据集上预训练的ViT迁移到ViViT的方法。

Positional embeddings

位置嵌入\(\mathbf{p}\)被添加到每个输入token。 但是，视频模型比预训练的图像模型多\(n_t\)倍的token。因此，通过将它们从\(\mathbb{R}^{n_w \cdot n_h \times d}\)临时“重复”到\(\mathbb{R}^{n_t \cdot n_h \cdot n_w \times d}\)来初始化位置嵌入。 在初始化时，具有相同空间索引的所有token都具有相同的嵌入，然后进行微调。

Embedding weights, E

当使用“tubelet embedding”token化方法时，\(\mathbf{E}\)是一个3D张量，与预训练模型中的2D张量\(\mathbf{E}_{\text{image}}\)相比。用于视频分类的从2D滤波器初始化3D卷积滤波器的常用方法是通过沿时间维度复制滤波器并对它们进行平均来“膨胀”它们，如I3D。 \[ \mathbf{E} = \frac{1}{t}[\mathbf{E}_{\text{image}}, \ldots, \mathbf{E}_{\text{image}}, \ldots, \mathbf{E}_{\text{image}}]. \] 论文也提出了一种不一样的方式，称为“central frame initialisation”：除了中间帧，\(\mathbf{E}\)的其他帧都使用0来初始化， \[ \mathbf{E} = [\mathbf{0}, \ldots, \mathbf{E}_{\text{image}}, \ldots, \mathbf{0}]. \]

Transformer weights for Model 3

模型3的结构设计，是独立的空间attention和时序attention，空间attention可以直接使用图像模型的pretrain，时序attention初始化为0。