《Dynamic Spatio-Temporal Specialization Learning for Fine-Grained Action Recognition》阅读笔记
摘要、引言、结论
本文设计了一个新型动态时空专业化模块(Dynamic Spatio-Temporal Specialization,简称DSTS),该模块由只会被高度相似的样本子集所激活的专门神经元组成。为了在相似样本的特定子集中进行区分,损失将促使专门神经元专注于细粒度差异。
本文设计了一种时空专门化方法,为专门化神经元提供空间或时间专门化,使其每次只关注输入特征映射的每个通道的一个单一方面(空间或时间)。
而在端到端的训练中,需要训练两种类型的参数:upstream 参数(如评分核和门参数)用于做动态决策和downstream参数(如时空算子)用于处理输入。由于上流参数的训练也会影响到下流参数,因此本文设计了一种上游-下游学习的算法(UDL),学习如何做出对下游参数训练有积极影响的决策,提高DSTS模块的性能。
解决的问题:成功地区分具有细微差别的操作类别(细粒度设置中较高的类间相似性)
提出的方法
概述
对于每个输入样本,每层中只有一个专门神经元被激活——这种动态激活发生在论文所说的突触机制,而且这种突出机制使得每个专门的神经元旨在相似的样本子集上被激活。由于训练过程中,每个专门神经元只在包含相似样本的子集上训练,因此训练loss会促使专门的神经元去学习处理与这些样本相关的细粒度信息,而不是学到更多常见的辨别性线索。
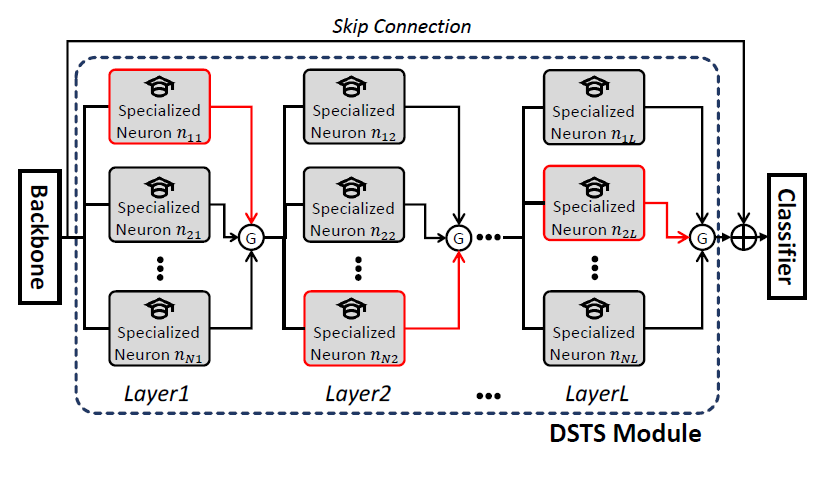
DSTS的图示如上,DSTS处理从backbone传过来的特征。DSTS模块内有L层,每一层都由N个专门化神经元组成。当特征映射X被输入到第j个DSTS层时,首先计算每个专门化神经元\(n_{ij}\)的脉冲值\(v_{ij}\),接着该层中具有最高脉冲值的神经元被Gumbel- Softmax激活。在被送入分类器之前,一个从backbone到输出的跳过连接被加到生成的特征。
为简单起见,将batchsize设置为1,假设预训练的backbone输出的特征图为\(X \in \mathbb{R}^{N_{i n} \times N_{t} \times N_{h} \times N_{w}}\),其中\(N_{i n}, N_{t}, N_{h}, N_{w}\)代表特征图的通道、时间、高度和宽度的维度。DSTS模块由L层组成,每层由N个专门的神经元组成。定义第j层的第i个专门神经元为\(n_{ij}\),每个专门的神经元\(n_{ij}\)都有一个评分核\(m_{i j} \in \mathbb{R}^{N_{\text {out }} \times N_{i n} \times 1 \times 1 \times 1}\)(大小为1×1×1,用于高效编码特征图X的所有通道的信息),一个由卷积核组成的空间算子\(S_{i j} \in \mathbb{R}^{N_{\text {out }} \times N_{\text {in }} \times 1 \times 3 \times 3}\),一个由卷积核组成的时间算子\(T_{i j} \in \mathbb{R}^{N_{\text {out }} \times N_{i n} \times 3 \times 1 \times 1}\),以及门\(g_{i j} \in \mathbb{R}^{N_{i n}}\)
DSTS层
突触机制
为了专业化效应的突触机制,每一个专门神经元上都包含一个用于在scoring convolution的输入特征图X的评分核。输出的结果会被求和以得到反映输入特征映射X与专门化神经元\(n_i\)的细粒度专门化能力之间的相关性得分,称之为脉冲\(v_i\)。专门化神经元产生的脉冲越高,专门化神经元的知识与输入特征的相关性越高,就越有可能被激活。
- 首先在X上应用一个评分核为\(m_i\)的卷积
\[ q_{i}=m_{i}(X) \]
其中,\(m_{i}(·)\)是评分卷积的简略表示,\(q_{i} \in \mathbb{R}^{N_{\text {out }} \times Q_{t} \times Q_{h} \times Q_{w}}\) 。
- 把\(q_i\)中的所有元素相加,就得到了特殊神经元\(n_i\)的脉冲\(v_i\)。
\[ v_{i}=\sum_{u_{c}=1}^{N_{\text {out }}} \sum_{u_{t}=1}^{Q_{t}} \sum_{u_{h}=1}^{Q_{h}} \sum_{u_{w}=1}^{Q_{w}} q_{i, u_{c}, u_{t}, u_{h}, u_{w}}\\ \mathcal{V}=\left\{v_{i}\right\}_{i=1}^{N} \]
在\(\mathcal{V}\)上应用Gumbel-Softmax技术来选择一个特定的神经元进行激活。
激活特定神经元\(n_a\)的选择是通过在所选指标a处产生一个具有1的one-hot向量来实现的。在训练过程中,Gumbel-Softmax允许梯度通过这种选择机制反向传播。在测试过程中,被激活的神经元\(n_a\)是在\(\mathcal{V}\)里具有最高脉冲的,以及具有最相关的专门化来区分与输入X相似的样本。
作者认为,突触机制对于专门神经元的专门化是至关重要的。卷积滤波器会对相似的特征图输入产生相似的想要,因此\(q_i\)和\(v_i\)对于相似的特征图会趋于相似。于是,在训练过程中,相似的特征图极有可能为相同的专门化神经元产生高脉冲得分(并激活);而这个神经元将只在相似样本的子集上被更新,这样就能使得这个神经元专门研究细粒度的差异来区分它们。
时空专门化
直观地说,在\(n_a\)被激活后,可以简单地在X上应用一个三维卷积核(对应于\(n_a\))来提取时空信息。但在细粒度动作识别,动作之间的细粒度差异会存在与动作的更多时空方面,因此还优化了专门化神经元的结构,以专门关注更多空间或更多时间的细粒度信息。
更具体地说,时空专门化方法适应专门化神经元的体系结构,为每个输入通道选择空间算子或时间算子。空间算符使用二维卷积集中在特征映射的空间方面,而时间算子使用关注时间方面的一维卷积。在训练过程中,这种架构设计使得每个专门神经元利用所选方面的相似样本之间每个通道的细粒度差异,这样能具有更好的敏感度。通过让模型调整架构来选择每个通道的操作子从而实现更大的识别能力,而这种架构决策是通过门参数来学习的,当专门神经元专注于某个方面是有益的,门参数将学会使用相应的运算子。
- Spatio-temporal Architectural Decisions using Gates
专门化神经元的门参数\(g_a\)由\(N_{in}\)个元素组成,每个元素对应一个输入通道。每个门参数决定了对应的通道是用空间还是时间算子处理的。
在正向传递过程中,使用改进的Semhash方法从门参数\(g_a\)中采样二进制决策,获得二进制向量\(\mathbf{b} \in\{0,1\}^{N_{i n}}\)。改进的Semhash方法使得我们可以以端对端的方式训练门参数\(g_a\)。我们把b的第l个元素表示为\(b_l\)。如果\(b_l\)为0则对应的输入通道\(l\)将使用空间算子,如果\(b_l\)为1则使用时间算子。
- Specialized Spatio-Temporal Processing
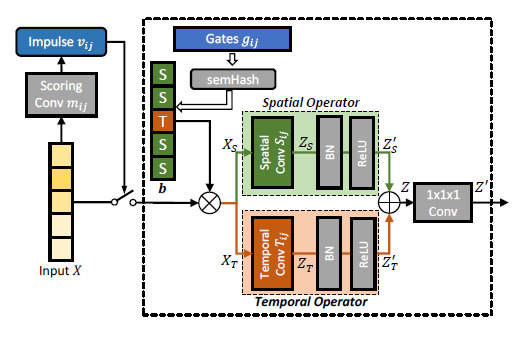
在获得通道型架构决策b后,可以从通道型输入特征映射X的选择开始,得到如下的特征\(X_S\)和\(X_T\),分别用于学习细粒度的空间和时间信息 \[ \begin{array}{r} X_{S}=(\mathbf{1}-\mathbf{b}) \cdot X, \\ X_{T}=\mathbf{b} \cdot X, \end{array} \] 其中\(\mathbf{1}\)是一个长度为\(N_{in}\)的向量,大小为1,而\(\cdot\)指的是沿通道维度的乘法,同时将\(b\)和\((1 - b)\)的每个元素视为一个通道。 \[ \begin{array}{l} Z_{S}=S_{a}\left(X_{S}\right) \\ Z_{T}=T_{a}\left(X_{T}\right) \end{array} \] 其中\(Z_S\)表示捕获输入特征图空间信息的特征\(X\),而\(Z_T\)表示捕获时间信息的特征。在经过一个bn层和ReLU层之后得到的特征为\(Z'_S\)和\(Z'_t\) ,输出特征图为两者之和。最后,对Z进行1 × 1 × 1卷积,融合空间和时间特征。而融合的特征\(Z'\)将作为下一层DSTS或分类器的输入。
上下游学习
为了进一步提高DSTS模块的性能,论文设计了一个UDL算法,该算法可以更好地优化与动态决策相关的模型参数,称之为上游参数。动态决策相关的上游参数(例如评分核\(m\)和门参数\(g\))和处理输入的下游参数(例如时空算子\(S\)和\(T\))会在端到端的训练中联合训练,而这的挑战主要是上游参数也会影响到下游参数的训练。因此,作者使用元学习(meta-learning)优化上游参数,同时考虑下游参数的影响,从而提高下游参数的学习能力,提高整体性能。
元学习算法由三步骤组成。第一步,通过更新下游参数的同时冻结上游参数从而模拟使用当前上游参数集进行动态决策时,下游参数的训练过程。第二步,在验证集上评估模型在held-out样本的性能。来自该评估的二阶梯度(相对于上游参数)提供了如何更新上游参数的反馈,以便它们在训练期间的动态决策可以改进下游参数的学习过程,从而在held-out样本上获得更好的性能。最后一步,使用元优化的上游参数对下游参数进行优化,这些参数现在在模型中做出动态决策,以便下游参数能够从训练中获得更多好处,并提高(测试)性能。
具体地说,在每一次迭代中,在训练数据中采样两个mini-batch:训练样本\(D_{train}\)和验证样本\(D_{val}\)。
Simulated Update Step:在\(D_{train}\)上使用监督loss更新下游参数\(d\) \[ \hat{d}=d-\alpha \nabla_{d} \ell\left(u, d ; D_{\text {train }}\right) \] 其中,\(\alpha\)为学习率超参数,\(u\)和\(d\)分别表示上游和下游参数。在这个步骤中\(u\)保持固定。
Meta-Update Step:在\(D_{val}\)中验证更新后的模型,当上游参数\(u\)在第一个模拟更新步骤中用于决策时,使用关于\(u\)的二阶梯度更新上游参数\(u\) \[ u^{\prime}=u-\alpha \nabla_{u} \ell\left(\hat{u}, \hat{d} ; D_{v a l}\right) \] 其中\(\hat{u}\)是\(u\)的副本,但不计算关于\(\hat{u}\)的梯度。这里需要计算的梯度指的是\(u^{\prime}\)关于\(\hat{d}\)中\(u\)的梯度,即二阶梯度。这些二阶梯度为如何调节\(u\)提供反馈以更好地训练下游参数,从而提高在不可见样本的性能。在这个步骤中\(d\)保持固定。
Actual Update Step:保持\(u^{\prime}\)冻结的情况下更新\(d\) \[ d^{\prime}=d-\alpha \nabla_{d} \ell\left(u^{\prime}, d ; D_{\text {train }}\right) \]
