Frequency Guidance Matters Skeletal Action Recognition by Frequency-Aware Mixed Transformer

摘要
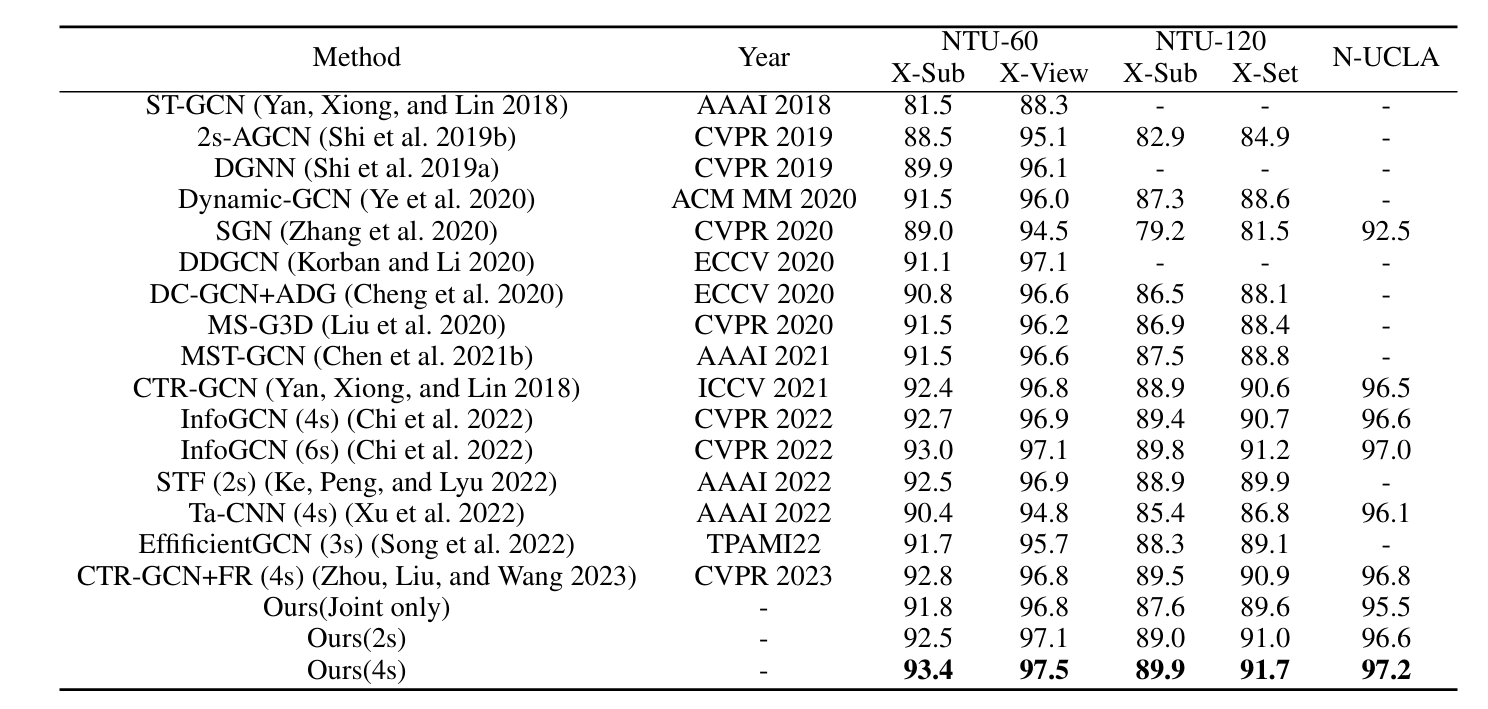
图卷积网络(GCNs)和transformer已被广泛应用于基于骨架的人体动作识别,每种网络在捕捉空间关系和长程依赖关系方面都具有独特的优势。然而,对于大多数GCN方法而言,拓扑结构的构建仅依赖于人体关节点的空间信息,限制了其直接捕获更丰富的时空依赖关系的能力。此外,许多Transformer方法的自注意力模块缺乏拓扑结构信息,限制了模型的鲁棒性和泛化性。为了解决这些问题,本文提出了一种联合轨迹图(Joint Trajectory Graph, JTG),将时空信息集成到一个统一的图结构中。本文还提出了一种联合轨迹图former (JT-GraphFormer),直接捕获所有关节轨迹之间的时空关系,用于人体行为识别。为了更好地将拓扑信息融入时空关系中。引入一种时空Dijkstra注意力(STDA)机制来计算JTG中所有关节的关系得分。此外,在分类阶段引入Koopman算子,以增强模型的表示能力和分类性能。实验表明,JT-GraphFormer在人体行为识别任务中取得了出色的性能,在NTU RGB+D、NTU RGB+D 120和N-UCLA数据集上的性能优于当前最先进的方法。
引言
论文认为的现有方法不足
首先,传统的GCN方法不能直接利用时空拓扑结构来捕获更全面的时空依赖关系。聚合图中邻近节点的信息以更新节点表示对于捕获空间依赖关系是有效的,而简单地扩展空间图并不足以有效地捕获时序动态关联。
其次,在关节坐标序列中,信息的密度可能在空间和时间维度之间变化,在时间维度上存在较大的冗余。
最后,自注意力机制虽然可以自适应地计算序列元素的相关性分数,但可能无法捕获每个序列元素的隐藏拓扑信息,导致模型的鲁棒性和泛化性受到负面影响。
解决方案
提出一种具有联合轨迹图(JTG)的Joint Trajectory GraphFormer(JT-GraphFormer)模型。JTG在原始空间图结构之上引入了时间维度,使其能够更好地封装与关节轨迹相关的复杂判别细节。与ST-GCN不同,JTG专注于构建一段时空周期内节点之间的拓扑结构。具体而言,构建某一帧序列内所有关节的动态轨迹拓扑,如图1 (a)所示。为了更有效地捕获复杂的时空依赖关系,JTG将连接扩展到相邻帧中的节点。该策略减少了冗余的时间信息,并利用统一的图结构捕获时空维度内的内在依赖,促进了跨时空域特征的聚集。
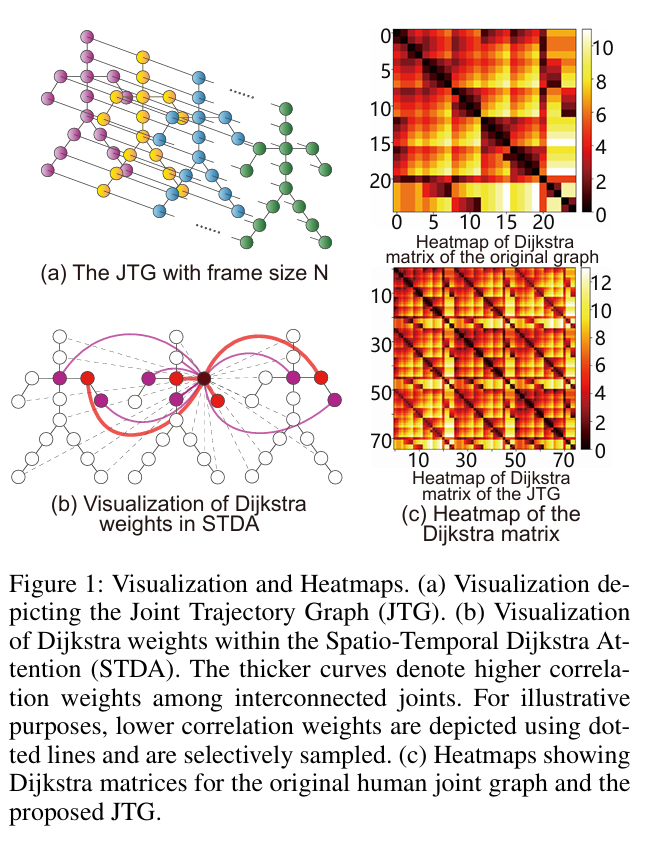
当使用JTG作为Transformer的输入时,单帧内的节点会同时计算相邻帧内所有节点的注意力,这对模型处理复杂的时空关联提出了较高的要求。作者受Graphormer中空间编码的启发,提出了一种时空Dijkstra注意力(STDA)机制,将JTG中关节之间的距离作为时空拓扑信息添加到注意力分数的计算中,这使每个节点能够学习更多地关注与动作更相关的邻居节点。STDA将全局注意力得分和最短路径权重相结合,通过加入关节轨迹中存在的先验信息,表现出更强的表达能力。节点与其邻居的相关权重如图1 (b)所示,Dijkstra矩阵的热图如图1 (c)所示。
此外,作者将Koopman算子引入到分类阶段。
The Koopman operator is a linear operator that describes a nonlinear dynamical system by map ping it into an infinite-dimensional Hilbert space.
Koopman算子是一种线性算子,通过将非线性动力系统映射到无限维希尔伯特空间来描述非线性动力系统。
贡献
• Introduction of JTG as an input data representation, leveraging trajectory information to enrich feature aggregation capabilities for nodes and their interactions across frames.
• Proposal of STDA, augmenting feature aggregation among neighboring nodes via the integration of shortest path concepts between joints.
• Incorporation of the Koopman operator for classifica tion, facilitating an encompassing perspective and supe rior classification performance.
• Rigorous evaluation of our proposed model across three diverse datasets (NTU RGB+D, NTU RGB+D 120, and N-UCLA), revealing its superiority over existing state of-the-art (SOTA) methods and underscoring its potential as a promising solution for action recognition tasks.
方法
Joint Trajectory Graph
将动作序列分成几个组。每个组有N个框架,并用图结构描述关节轨迹,称为Joint Trajectory Graph,\(G_{JT} = (G_t,G_{t+1},\ldots,G_{t+N-1},E_T) = (V_{JT},E_{JT})\) ,其中\(G_t\)是1帧中节点的空间图,\(E_T\)是对应的边集合,表示N帧中节点的关节轨迹,\((V_{JT},E_{JT})\)分别表示JTG中的节点和边集合。 \[ A_{JT}=\begin{bmatrix}A&A+I&A&\cdots&A\\A+I&A&A+I&\ddots&\vdots\\A&A+I&\ddots&\ddots&A\\\vdots&\ddots&\ddots&A&A+I\\A&\cdots&A&A+I&A\end{bmatrix} \]
A为框架中所有关节的物理连通性,I为单位对角矩阵,表示相邻框架中相同关节的连通性。
JT-GraphFormer
Positional Encoding
\(X\in\mathbb{R}^{C\times T\times V}\) ========> \(X\in\mathbb{R}^{C\times T/N\times V*N}\)
在JTG中,关节的运动轨迹涉及特定的时间信息,因此需要为每个帧进行位置编码(PE),以正确地表达顺序关系。 \[ \begin{aligned}&PE(p,2i)=\sin(p/10000^{2i/C_{in}}),\\&PE(p,2i+1)=\cos(p/10000^{2i/C_{in}}),\end{aligned} \]
STDA Module
作用:将时空拓扑信息引入多头注意力机制,增加了邻居节点之间关联的权重,从而使节点更偏向于聚合局部邻居的特征。
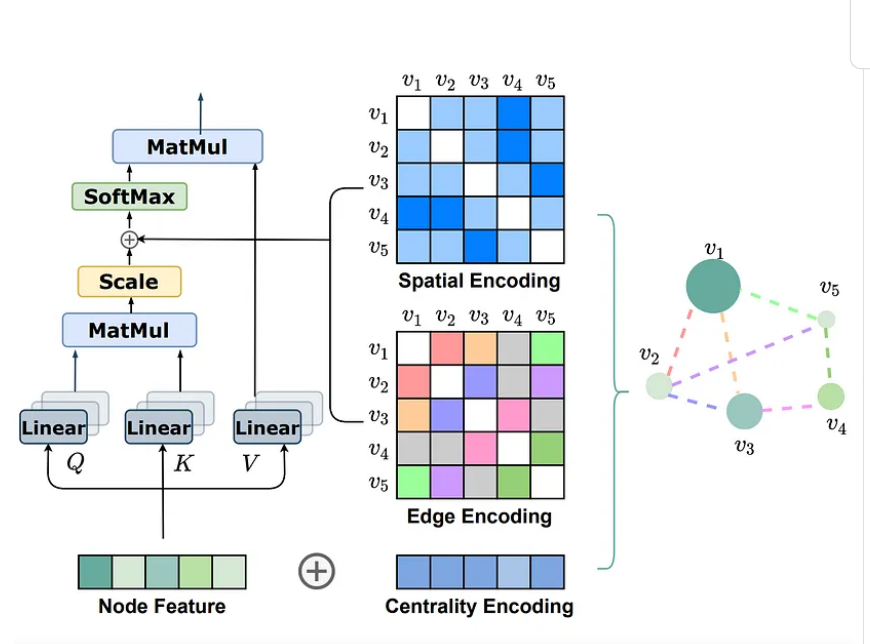
作者说受到Graphormer空间编码的启发,但实际上还是不一样的。
| Graphormer | STDA Module |
|---|---|
 |
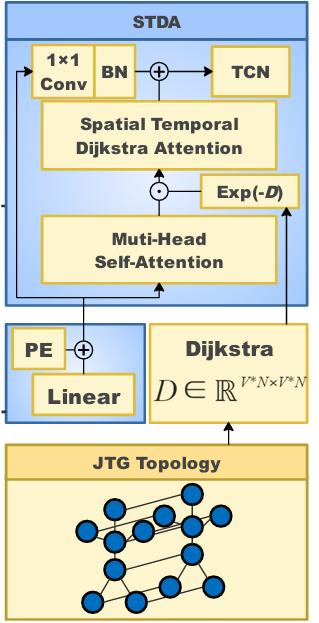 |
公式: \[ \begin{array}{l} W=\exp(-D)+b,\\a_{map}=Tanh(QK^T/\sqrt{d_K}\times\alpha),\\a_{score}=a_{map}\cdot W,\end{array} \]
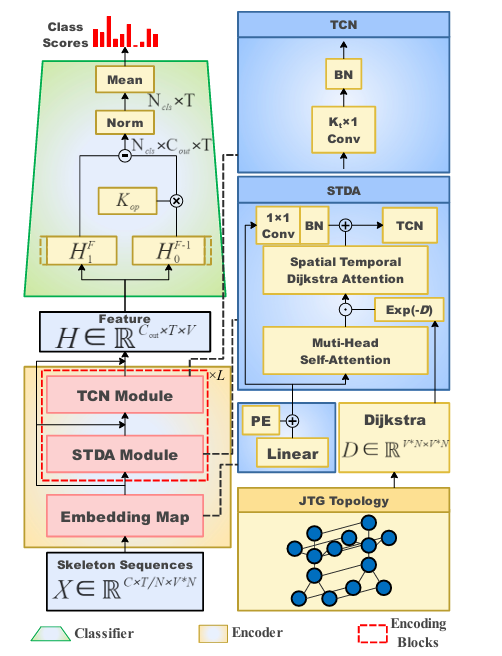
Koopman Operator
Koopman算子是一个将非线性动力系统映射到无限维希尔伯特空间的线性算子。这种映射允许在线性空间中描述系统的演化,比原始的非线性空间更容易分析
在深度学习中,利用Koopman算子提取非线性动力系统的演化特征以提高分类性能。本文建立了时间演化函数\(f(\cdot)\),用于JT-GraphFormer跨不同帧的输出特征\(H\),将第\(t\)帧的特征\(h_t\)与下一帧的特征\(h_{t+1}\)联系起来,即\(h_{t+1} = f(h_t)\)。
将Koopman算子\(K_{op}\)定义为一个\(N_{cls} × C_{out} × C_{out}\)线性算子,其中\(N_{cls}\)表示动作类别的数量,\(C_{out}\)表示最后一个JT-GraphFormer块的输出通道数量。\(K_{op}\)应用线性方法来近似时间维度上各类动作特征之间的相互关系,满足等式: \[ h_{t+1}\approx K_{op}h_t \] 由于我们在不同的帧步建立了线性相关性,因此可以近似表示任意连续帧段的特征\(H_x^y\),即从第\(x\)帧到第\(y\)帧的特征段。因此特征\(H_1^{T-1}\)可以表示为: \[ H_1^{T-1}\approx[h_1,K_{op}h_1,K_{op}^2h_1,\cdots,K_{op}^{T-2}h_1]\\ H_{t+1}^T\approx K_{op}H_t^{T-1} \] 采用DMD算法,通过最小化\(\| H_2^T- K_{op}H_1^{T- 1}\| _2\)的Frobenius范数来更新\(K_{op}\)。由于\(K_{op}\)表示各个动作类别的特征演化,我们可以对\(K_{op}\)在时间维度上进行平均,从而得到每个类别的概率分布,最终完成分类。
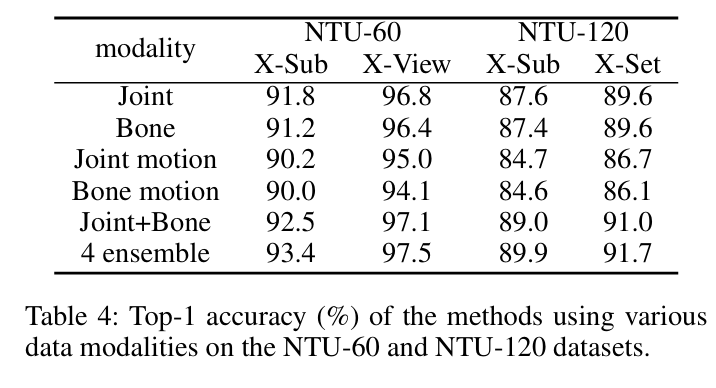
实验
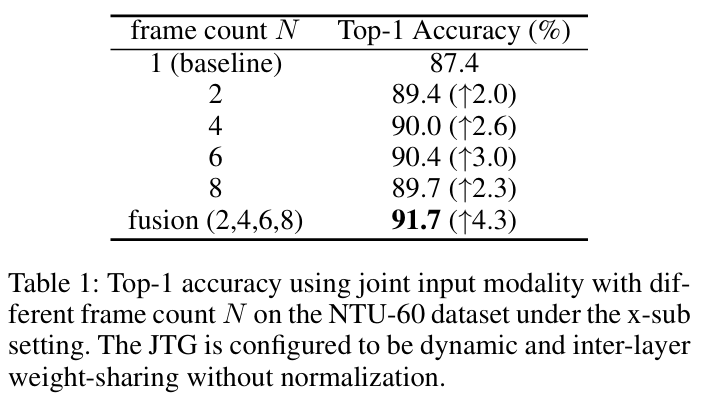

研究了JTG结构的静态和动态配置之间的性能差异,以及是否采用层间共享权重。此外,对JTG是否需要归一化进行了探讨。
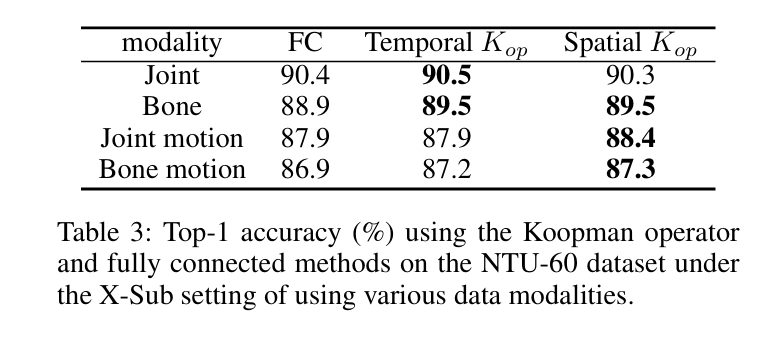
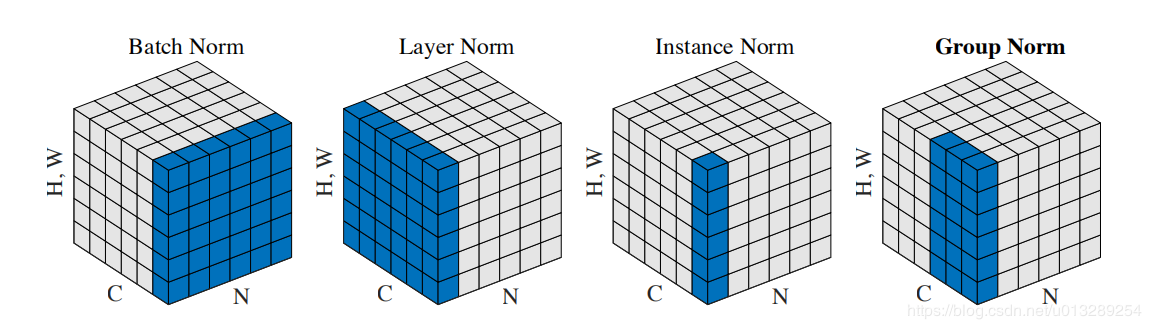 # 为什么要归一化
# 为什么要归一化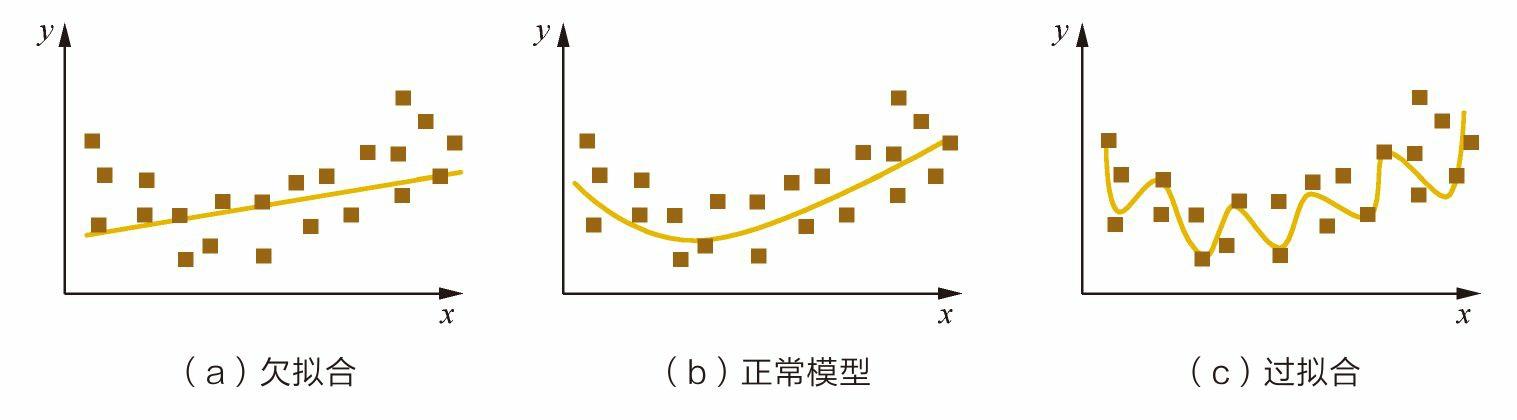 ##
过拟合
##
过拟合